A Tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB (a) subtends an angle of 60∘ at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30°. The height of the tower is Solution in Telugu
2a√3
2a√3
a√3
a√3
The correct Answer is:C
Step by step video, text & image solution for A Tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB (a) subtends an angle of 60^(@) at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30°. The height of the tower is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - REVISION EXERCISEEXERCISE - HYPERBOLIC FUNCTIONS10videos
REVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - REAL FUNCTIONS EXERCISE - EXERCISE-134videos
REAL FUNCTIONS
- BOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II (ADVANCED) PRACTICE SHEET (ADDVANCED)) (Comprehension Type Questions)6videos
STRAIGHT LINES
Similar Questions
cosech−1(32)+cosech−1(−12)=
02:12View SolutionFind the domains of the following functions
f(x)=x2+x+103:21View SolutionLet A(0,0), B (5,0), C (5,3) and D(0,3) be the vertice of rectiangle ABCD , If P is a variable point lying inside the rectangle ABCD and d (P,L) denotes perpendicular distance of point P from line L
If ≤min{d(P,BC),d(P,CD),d(P,AD)}, then area of the region in which P lies is (in sq. units01:54View SolutionABC is a triangular park with AB=AC=100m. A Television tower stands at the mid point of BC. The angles of elevations of the top of tower at A,B,C are 45∘,60∘,60∘ respectively Then the height of tower is
02:58View SolutionThe Heights of two tower are 180 metres and 60 metres respectively. If the angle of elevation of the top of the first tower from the foot of the second tower is 60∘. Calculate the angle of elevation of the top of the second tower from the foot of the first.
04:28View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
04:21View Solutionएक मीनार के पाद से 40 मीटर दुरी पर स्तिथित किसी बिनु से मीनार के शिखर का उनयन कोण 30∘ है मीनार की उचाई ज्ञात कीजिएः
01:36View SolutionThe angles of elevation of the tops of two vertical towers as seen from the middle point of the line joining the foot of the towers are 60^@,30^@ respectively. The ratio of the heights of the towers is
01:49View SolutionA vertical tower subtends an angle of 60∘ at a point on the same level as the foot of the tower. On moving 100 m further in line with the tower, it subtends an angle of 30∘ at the point. Then, the height of the tower, it subtends an angle of 30∘ at the point. Then, the height of the tower is
01:33View SolutionAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
02:19View SolutionFrom a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ . The height of the tower is
04:21View SolutionA tower stands vertically on the ground. From a point on the ground, 20m away from the foot of the tower, the angle of elevation of the top of the tower is 60∘ . What is the height of the tower?
04:10View SolutionThe angle of elevation of the top of a tower from a point on the ground 30m away from the foot of the tower is 30∘. Then, the height of the tower is ……..m
02:39View SolutionA tower is at the center of a circular Bigache. A and B are two points on the edge of the garden such that AB (= a) is at the foot of the tower. 60^(@) The angle of elevation and the elevation angle of the top of the tower from A or B 30^(@) is. The height of the tower is.
View SolutionThe angle of elevation of the top of a tower from a point A on the ground is 30∘. On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to 60∘. Find the height of the tower and distance of the tower from the point A.
03:02View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
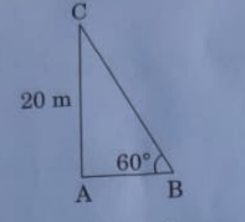 01:18View Solution
01:18View Solution
