A tower stands at the centre of a circular park .A and B are two points on the boundary of the park such that AB = (=a) subtends an angle of 60∘ at the foot of the tower ,and the angle of elevation of the top of the tower from A or B is 30∘ the height of hte tower is Solution in Tamil
a√3
a√3
2a√3
2a√3
The correct Answer is:A
Step by step video, text & image solution for A tower stands at the centre of a circular park .A and B are two points on the boundary of the park such that AB = (=a) subtends an angle of 60^@ at the foot of the tower ,and the angle of elevation of the top of the tower from A or B is 30^@ the height of hte tower is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE
44 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - NEW JOYTHI PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Objective
36 Videos
- VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - CONTINUOUS EVALUATION
2 Videos
Similar Questions
The equation sec2θ=4xy(x+y)2 is possible for x,y, ∈R only if
View SolutionThe distance between x axis and the point (3,12,5) is
View SolutionComplete the table

View SolutionABC is a triangular park with AB=AC=100m. A Television tower stands at the mid point of BC. The angles of elevations of the top of tower at A,B,C are 45∘,60∘,60∘ respectively Then the height of tower is
View SolutionA tower subtends and angle 60^(@) at a point A in the plane of its base and the angle of depression of the foot of the tower at a point 10 meters just above A is 30^(@). The height of the tower is
View SolutionA vertical tower PQ subtends the same anlgle of 30∘ at each of two points A and B ,60 m apart on the ground .If AB subtends an angle of 120∘ at p the foot of the tower ,then find the height of the tower .
View SolutionA tower subtends an angle of 60∘ at a point on the same level as the foot of the tower and at a second point just 10 meters above the first point the angle of depression of the foot of the tower is 15∘. The height of the tower is (in meters)
View SolutionABC एक त्रिभुजाकार पार्क है, जहाँ AB=AC=100 मी | एक दूरदर्शन टॉबर (television tower) BC के मध्य - बिन्दु पर खड़ा है | बिन्दु A, B व C से टॉवर के शीर्ष के उन्नयन कोण क्रमशः 45∘,60∘ व 60∘ है | टॉर्चर की ऊँचाई ज्ञात कीजिए |
View SolutionA vertical tower subtends an angle of 60∘ at a point on the same level as the foot of the tower. On moving 100 m further in line with the tower, it subtends an angle of 30∘ at the point. Then, the height of the tower, it subtends an angle of 30∘ at the point. Then, the height of the tower is
View SolutionA vertical pole stands at a point A on the boundary of a circular park of radius 2 km and subtends an angle 60∘ at another point B on the boundary. If the chord AB subtends the same angle 60∘ at the centre of the park, the height of the pole is
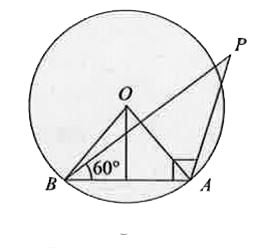
View SolutionA tower PQ subtends an angle α at a point A on the same level as the foot Q of the tower. It also subtends the same angle α at a point B where AB subtends the angle α with AP then
View SolutionABCD is a rectangular park with AB = a. A tower standing at C makes angles αandβ at A and B respectively, the height of the tower is
View SolutionA pole stands at a point A on the boundary of a circular park of radius a and subtends an angle α at another point B on the boundary. If the chord AB subtends an angle α at the centre of the path, the height of the pole is
View SolutionA vertical pole stands at a point A on the boundary of a circular park of radius a and subtends an angle α at another point β on the boundary. If the chord AB subtends an angle α at the centre of the park, the height of the pole is
View SolutionA vertical tower PQ subtends the same anlgle of 30∘ at each of two points A and B ,60 m apart on the ground .If AB subtends an angle of 120∘ at p the foot of the tower ,then find the height of the tower .
View SolutionA tower is at the center of a circular Bigache. A and B are two points on the edge of the garden such that AB (= a) is at the foot of the tower. 60^(@) The angle of elevation and the elevation angle of the top of the tower from A or B 30^(@) is. The height of the tower is.
View Solution
