AC and BD are chords of a circle which bisect each other. Prove that i AC and BD are diameters ii ABCD is rectangle.
Given : A circle with chords AB and CD which bisect each other at O. To Prove : i AC and BD are diameters ii ABCD is a rectangle. Proof : In ∆OAB and ∆OCD we have OA = OC [Given] OB = OD [Given] ∠AOB = ∠COD [Vertically opposite angles] ⇒ ∆AOB ≅ ∠COD [SAS congruence] ⇒ ∠ABO = ∠CDO and ∠BAO = ∠BCO [CPCT] ⇒ AB || DC ... i Similarly we can prove BC || AD ... ii Hence ABCD is a parallelogram. But ABCD is a cyclic parallelogram. ∴ ABCD is a rectangle. [Proved in Q. 12 of Ex. 10.5] ⇒ ∠ABC = 90° and ∠BCD = 90° ⇒ AC is a diameter and BD is a diameter [Angle in a semicircle is 90°] Proved.
Related Solutions
AC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
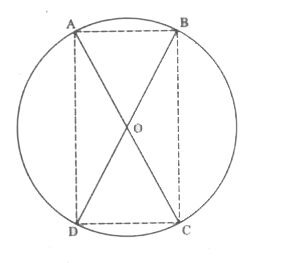
View SolutionAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
View SolutionAC और BD एक वृत्त की जीवाएं है जो परस्पर समध्दिभाजित करती है। सिद्ध कीजिए (i) AC और BD व्यास है (ii) ABCD एक आयत है।
View SolutionAC और BD एक वृत्त की जीवाऍ है जो परस्पर समद्विभाजित करती है । सिद्ध कीजिए
(i) AC और BD व्यास है , (ii) ABCD एक आयत है ।
View SolutionAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD arediameters, (ii) ABCD is a rectangle
View SolutionAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD arediameters, (ii) ABCD is a rectangle
View Solutionare chords of a circle which bisect each other. Prove that (i) are diameters (ii) is a rectangle.
View Solutionare chords of a circle which bisect each other. Prove that (i) are diameters (ii) is a rectangle
View SolutionAC and BD are chord of a circle which bisect each other. Prove that
(i) AC and BD are diameters.
View SolutionAC और BD एक वृत्त की जीवाएँ हैं, जो परस्पर समद्विभाजित करती हैं| सिद्ध कीजिए :
(i ) AC और BD व्यास हैं
View Solutionare chords of a circle that bisect each other. Prove that:AC and BD are diameter. ABCD is a rectangle
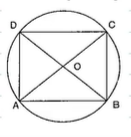
View SolutionAC and BD are chord of a circle which bisect each other. Prove that
(ii) ABCD is a rectangle.
View SolutionIf AC and BD are two chords of a circle that bisect each other then quadrilateral ABCD is a
View Solutionवृत्त ABCD का BD व्यास है, जो जीवा AC को बिंदु E पर समद्विभजित करता है। यदि जीवा AC = 8.0 सेमी तथा BE = 2.0 सेमी तो वृत्त की त्रिज्या ज्ञात कीजिये।
View SolutionAC এবং BD দুটি জ্যা পরস্পরকে O বিন্দুতে ছেদ করেছে। প্রমাণ করো, ABCD একটি আয়তক্ষেত্র।
View SolutionIs quadrilateral a ||gm?
I. Diagonals and bisect each other.
II. Diagonals and are equal.
View SolutionAC ಮತ್ತು BD ವೃತ್ತ ಜ್ಯಾಗಳು ಪರಸ್ಪರ ಅರ್ಧಿಸುತ್ತವೆ. ಹಾಗಾದರೆ. ABCD ಆಯತವಾಗಿದೆ ಎಂದು ಸಾಧಿಸಿ.
View SolutionABCD is a rectangle and AC & BD are its diagonals. If AC = 10 cm, then BD is:
View SolutionABCD is a rectangle in which diagonal AC bisects as well as Show that
(i) ABCD is a square
(ii) diagonal BD bisects
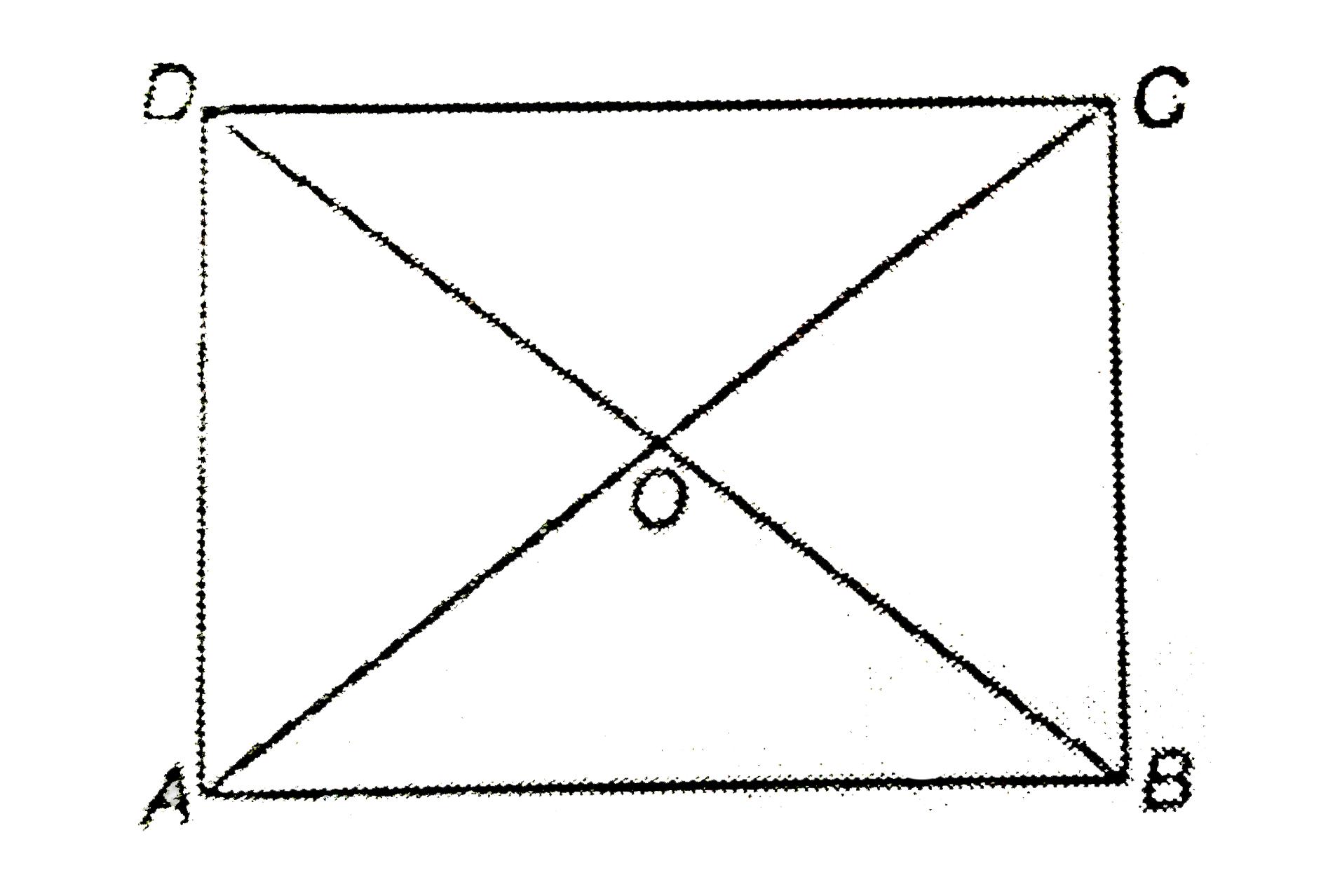
View SolutionABCD is a rectangle in which diagonal AC bisects /_C. Show that ABCD is a square.
View Solution