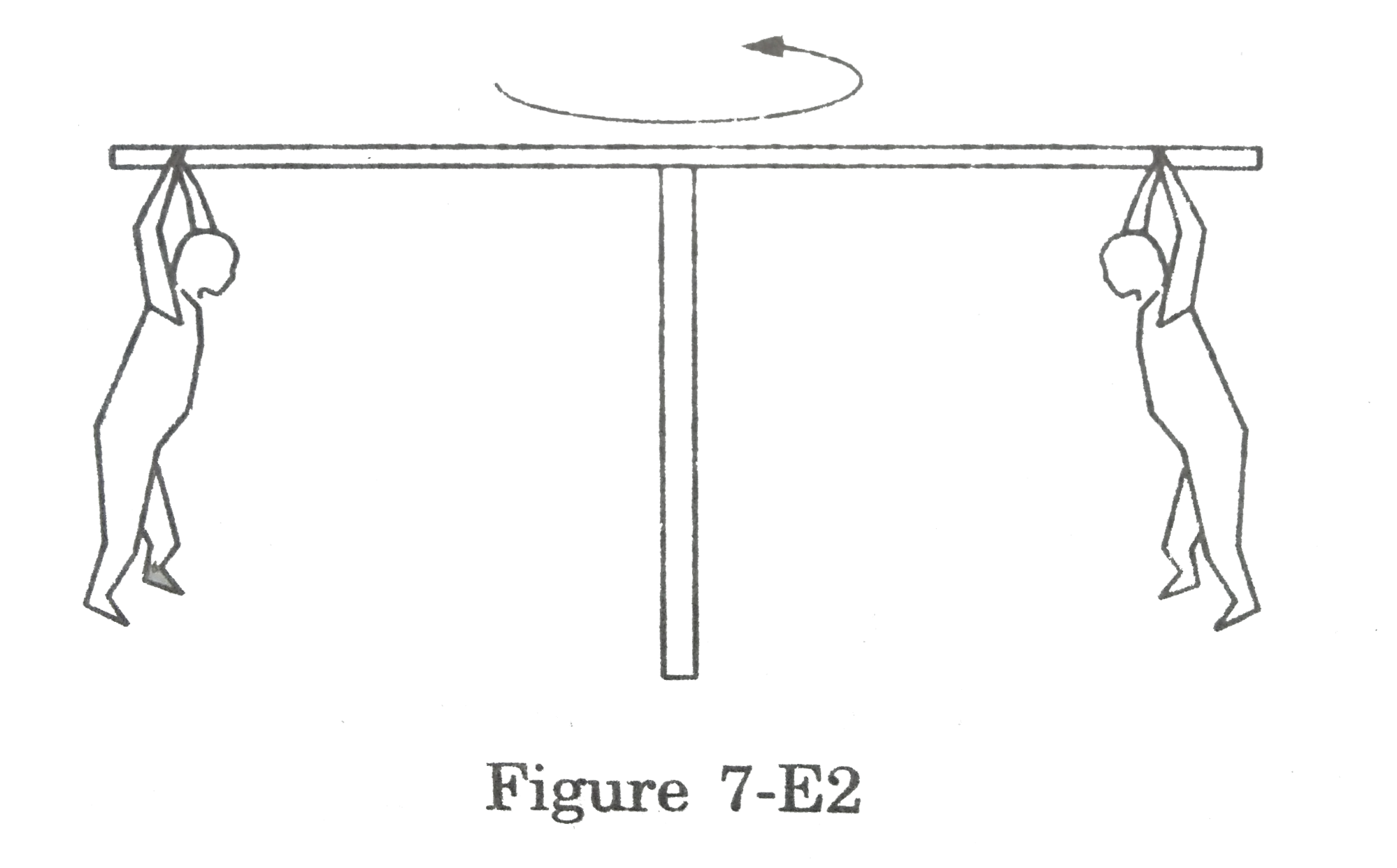
In a childrens park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod figure 7-E2. Let the mass of each kid be 15 kg the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
Frictional force on one of the kids is 10π2
Related Solutions
In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod figure. Let the mas of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
View SolutionIn a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod figure. Let the mas of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.

View SolutionIn a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so tht the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod figure. Let the mas of each kid be 15 kg, the distance betweent eh points of the rod where the two kids hold it be 3.0 m and supose that teh rod rotates at the rate of 20 revolutions per minute. Find the force of fircton exerted by te rod on one of the kids.

View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is omega . The force applied on the rod by the pivot is
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is omega . The force applied on the rod by the pivot is
View SolutionA homogenous rod XY of length L and mass 'M' is pivoted at the centre 'C' such that it can rotate freely in vertical plane. Initially the rod is in the horizontal position.
View Solution
A uniform rod of length and mass is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View Solution
A uniform rod of length and mass is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View SolutionTwo blocks each of the mass m are attached to the ends, a massless rod which pivots as shown in figure. Initial the rod is held in the horizontal position and then release, Calculate the net torque on this system above pivot.
View SolutionTwo blocks each of the mass m are attached to the ends, a massless rod which pivots as shown in figure. Initial the rod is held in the horizontal position and then release, Calculate the net torque on this system above pivot.
View SolutionA ligh rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.

View SolutionA light rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.

View SolutionA light rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.

View SolutionA particle is attached to an end of a rigid rod. The other end of the rod is hunged and the rod rotates always remaining horizontal. Its angular speed is increasing at contant rate. The mass of the particle is . The force exerted by the rod on the particle is , then:
View SolutionA particle is attached to an end of a rigid rod. The other end of the rod is hunged and the rod rotates always remaining horizontal. Its angular speed is increasing at contant rate. The mass of the particle is . The force exerted by the rod on the particle is , then:
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O . A horizontal force acts at the bottom of the rod. a. Find the angular velocity of the rod as the function of angle of rotation theta. b.What is the maximum angular displacement of the rod?
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O . A horizontal force acts at the bottom of the rod. a. Find the angular velocity of the rod as the function of angle of rotation theta. b.What is the maximum angular displacement of the rod?
View SolutionA slender rod of mass and length rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse perpendicular to the rod at other end is
View SolutionA slender rod of mass M and length L rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse J perpendicular to the rod at other end is
View SolutionA uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is. .
View Solution