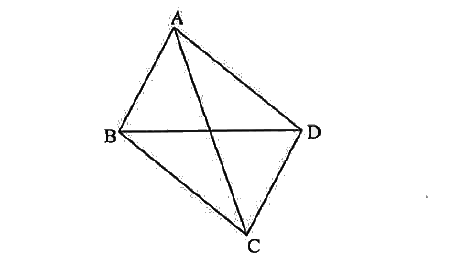
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD
Given : ABC and ADC are two right triangles with common hypotenuse AC. To Prove : ∠CAD = ∠CBDProof : Let O be the mid-point of AC. Then OA = OB = OC = OD Mid point of the hypotenuse of a right triangle is equidistant from its vertices with O as centre and radius equal to OA draw a circle to pass through A B C and D. We know that angles in the same segment of a circle are equal. Since ∠CAD and ∠CBD are angles of the same segment. Therefore ∠CAD = ∠CBD. Proved.
Related Solutions
ABC and ADC are two right triangle with common hypotenuse AC. Prove that CAD = CBD.
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that
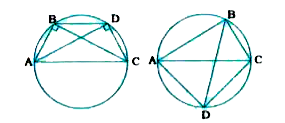
View Solutionउभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC है, सिध्द कीजिए कि है।
View Solutionउभयनिष्ट कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC है । सिद्ध कीजिए कि है।
View SolutionAC is the common hypotneus of the right-angled triangels ABC and ADC. Prove that
View Solutiontriangle ABC and triangle ADCs are two right-angled triangles with common diagonal AC /_ CAD = /_CBD Prove that.
View SolutionABC ও ADC সমকোণী ত্রিভুজদুটির সাধারণ অতিভুজ AC , প্রমাণ করো যে
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that /_CBD.
View SolutionAND are two right triangles with common hypotenuse Prove that
View Solutionand are two right triangles with common hypotenuse Prove that
View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that
View Solutionএবং হল দুটি সমকোণ যাদের সাধারণ অতিভুজ হলো AC । প্রমাণ করো, ।
View SolutionABC and DBC are two right angled triangles with common hypotenuse BC with their sides AC and BD intersecting at P. Prove that:
.
View SolutionIf is the mid-point of the hypotenuse of a right triangle prove that
View SolutionRight triangle /_\ABC Of /_A= 90^@ . AD perpendicular to the hypotenuse BC. Prove that (/_\ABC)/(/_\ACD)=(BC^2)/(AC^2)
View Solutionएक समकोण त्रिभुज ABC के कर्ण AC का मध्य बिन्दु D है तो सिद्ध करें कि
View SolutionShow that in a right triangle the hypotenuse is the longest side. GIVEN : A right triangle in which TO PROVE : Hypotenuse is the longest side, i.e. (ii)
View Solutionयदि D समकोण त्रिभुज ABC के कर्ण AC का मध्य-बिन्दु हों,तो सिध्द करो कि
View SolutionIf BD is the perpendicular drawn from the vertex B of the right triangle ABC to the hypotenuse AC,prove that(iii)
View Solutionएक समकोण त्रिभुज ABC में कर्ण, AC पर लंब BD खींचा गया है। सिद्ध करे की
View Solution