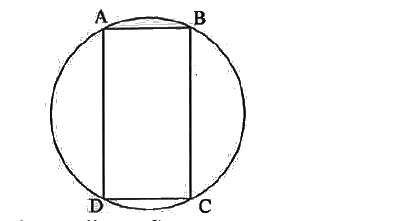
Prove that a cyclic parallelogram is a rectangle.
Given : ABCD is a cyclic parallelogram. To prove : ABCD is a rectangle. Proof : ∠ABC = ∠ADC ...i [Opposite angles of a ||gm are equal] But ∠ABC + ∠ADC = 180° ... ii [Sum of opposite angles of a cyclic quadrilateral is 180°] ⇒ ∠ABC = ∠ADC = 90° [From i and ii] ∴ ABCD is a rectangle [A ||gm one of whose angles is 90° is a rectangle] Hence a cyclic parallelogram is a rectangle. Proved.
Related Solutions
Prove that a cyclic parallelogram is a rectangle.
View SolutionProve that a cyclic parallelogram is a rectangle.
View SolutionProve that a cyclic parallelogram is a rectangle.
View SolutionProve that the cyclic parallelogram is a rectangle.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionProve that a cyclic parallelogram must be a rectangle.
View SolutionProve that a parallelogram which is not a rectangle is not cyclic.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionIf a parallelogram is cyclic, then it is a rectangle. Justify.
View SolutionIf a parallelogram is cyclic, then it is a rectangle. Justify.
View SolutionIf a parallelogram is cyclic, then it is a rectangle. Justify.
View SolutionIf a parallelogram is cyclic, then it is a rectangle. Justify.
View Solutionसिद्ध कीजिए की एक चक्रीय चतुर्भुज समांतर चतुर्भुज का आयत होता है।
View Solutionसिद्ध करें कि प्रत्येक आयत चक्रीय होता है।
View SolutionA cyclic parallelogram is a rectangle, then its diagonals are equal
View Solutionఒక సమాంతర చతుర్భుజం చక్రియమైన, అది దీర్ఘచతురస్రం అవుతుంది. సమర్థించండి.
View Solutionसिध्द कीजिए कि चक्रीय कि चक्रीय समांतर चतुर्भुज आयत होता है।
View Solutionਸਿੱਧ ਕਰੋ ਕਿ ਚੱਕਰੀ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਇੱਕ ਆਇਤ ਹੁੰਦਾ ਹੈ।
View Solution