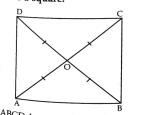
Show that the diagonals of a square are equal and bisect each other at right angles
Given : ABCD is a square in which AC and BD are diagonals. To Prove : AC = BD and AC bisects BD at right angles i.e. AC ⊥ BD. AO = OC OB = OD Proof : In ∆ABC and ∆BAD AB = AB [Common] BC = AD [Sides of a square] ∠ABC = ∠BAD = 90° [Angles of a square] ∴ ∆ABC ≅ ∆BAD [SAS congruence] ⇒ AC = BD [CPCT] Now in ∆AOB and ∆COD AB = DC [Sides of a square] ∠AOB = ∠COD [Vertically opposite angles] ∠OAB = ∠OCD [Alternate angles] ∴ ∆AOB ≅ ∆COD [AAS congruence] ∠AO = ∠OC [CPCT] Similarly by taking ∆AOD and ∆BOC we can show that OB = OD. In ∆ABC ∠BAC + ∠BCA = 90° [ ∠B = 90°] ⇒ 2∠BAC = 90° [∠BAC = ∠BCA as BC = AD] ⇒ ∠BCA = 45° or ∠BCO = 45° Similarly ∠CBO = 45° In ∆BCO. ∠BCO + ∠CBO + ∠BOC = 180° ⇒ 90° + ∠BOC = 180° ⇒ ∠BOC = 90° ⇒ BO ⊥ OC ⇒ BO ⊥ AC Hence AC = BD AC ⊥ BD AO = OC and OB = OD. Proved.
Related Solutions
Show that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
View SolutionIn figure, Show that if the diagonals of a quadrilateral are equal and bisect each other at right angle, then it is a square.
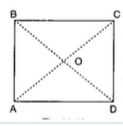
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View Solutionदर्शाइए कि एक वर्ग के विकर्ण बराबर होते है। और परस्पर समकोण पर समद्विभाजित करते हैं।
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
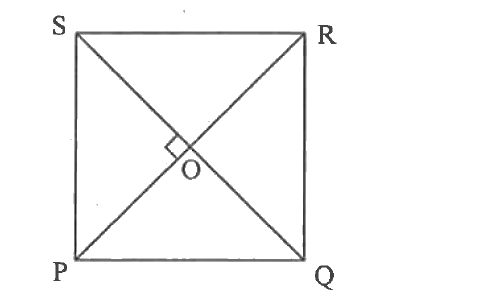
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angles then it is a square.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angle, then it is a square.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
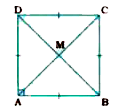
View SolutionShow that if the diagonals of a quadrilateral are equal and bisects each other at right angles, then it is a square.
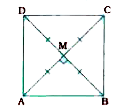
View SolutionShow that if the diagonals of a quadrilateral are qual and bisect each other at right angles, then it is a square
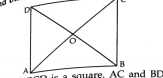
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles
View Solutionदर्शाये की वर्ग के विकर्ण समान लम्बाई के होते है और एक दूसरे को समकोण पर सदमद्विभाजित करती है।
View Solutionਦਰਸਾਉ ਕਿ ਇੱਕ ਵਰਗ ਦੇ ਵਿਕਰਣ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ ਅਤੇ ਆਪਸ ਵਿੱਚ ਸਮਕੋਣ 'ਤੇ ਸਮਦੁਭਾਜਿਤ ਕਰਦੇ ਹਨ।
View Solution