An ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p = kV. Show that the molar heat capacity of the gas for the process is given by C = Cv + R/2•
P=KV=>nRT/V=KV
Related Solutions
An ideal gas is taken through a process in which the pressure and the volume are changed according to the equation . Show that the molar heat capacity of the gas for the process is given by .
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation . Show that the molar heat capacity of the gas for the process is given by .
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation . Show that the molar heat capacity of the gas for the process is given by .
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation . Show that the molar heat capacity of the gas for the process is given by .
View SolutionAn ideal gas is taken through a process in which pressure and volume vary as . Show that the molar heat capacity of the gas for the process is given by .
View SolutionAn ideal gas is taken through a process in which pressure and volume vary as P = kV^(2) . Show that the molar heat capacity of the gas for the process is given by C = C_(v) +(R )/(3) .
View SolutionThe molar heat capacity for the process shown in fig. is
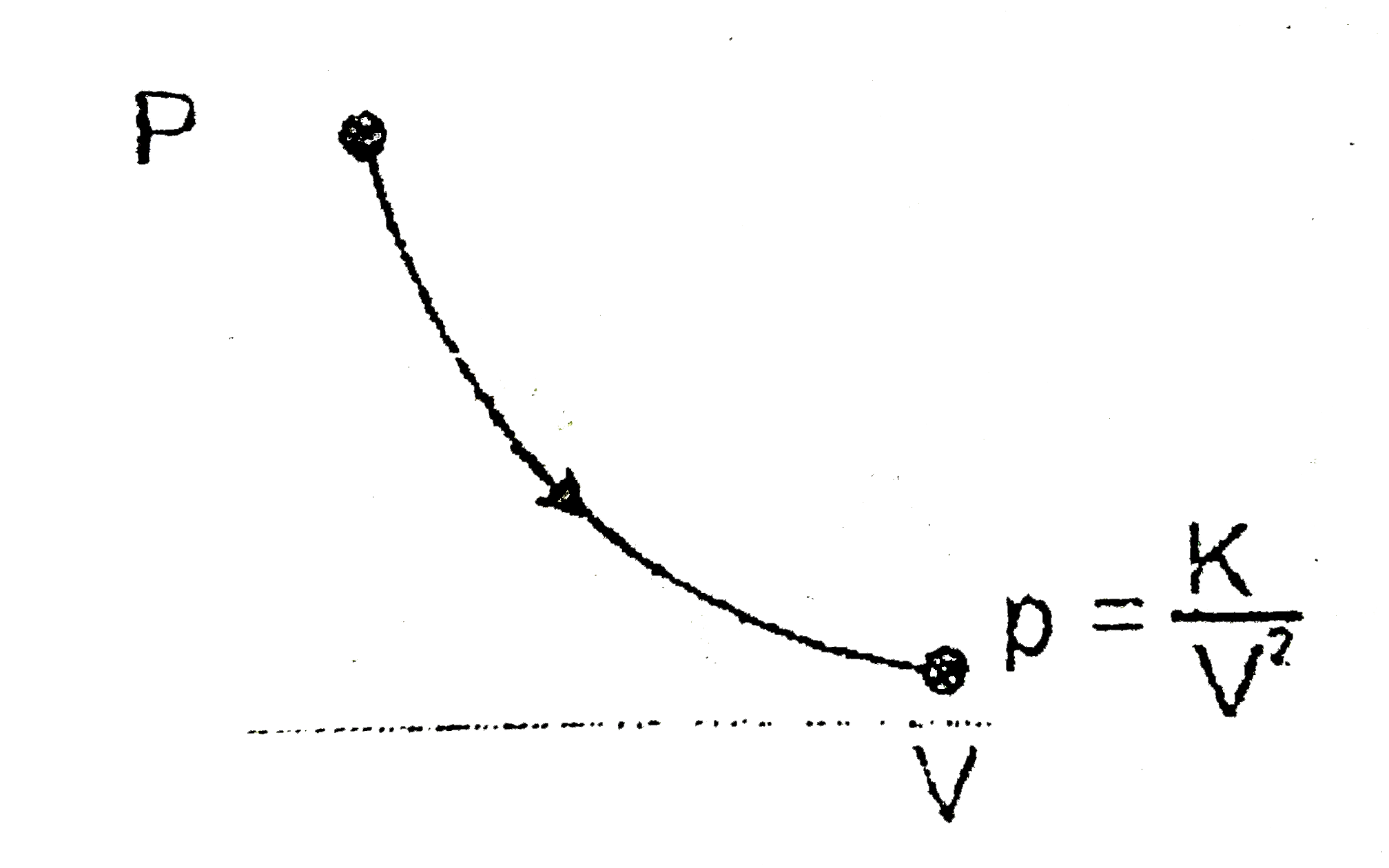
View SolutionFigure shows a process on a gas in which pressure and volume both change. The molar heat capacity for this process is C.
View SolutionAn ideal gas is taken through a process in which the process equation is given as P=kV^(alpha) , where k and alpha are positive constants. Find the value of alpha for which in this process molar heat capacity becomes zero.
View SolutionAn ideal diatomic gas undergoes a process in which the pressure is proportional to the volume. Calculate the molar specific heat capacity of the gas for the process.
View SolutionAn ideal diatomic gas is taken through a process in which the pressure and the volume vary as P = aV^b . If the specific heat capacity in the process is zero, then (-5b) is equal to ______
View SolutionFor certain process the molar heat capacity of an ideal gas is found to be (C_v+R/2) , where C_v is the molar heat capacity of the same gas at constant volume. For the given process, it can be concluded that
View SolutionFor certain process the molar heat capacity of an ideal gas is found to be (C_v+R/2) , where C_v is the molar heat capacity of the same gas at constant volume. For the given process, it can be concluded that
View SolutionIdeal mono-atomic gas is taken through process such that dQ = 3dU. The molar heat capacity for process is:
View SolutionIdeal mono-atomic gas is taken through process such that dQ = 3dU. The molar heat capacity for process is:
View SolutionA monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as constant. What will be the molar heat capacity of gas for this process?
View SolutionA monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV^(-3)= constant. What will be the molar heat capacity of gas for this process?
View SolutionA monatomic gas undergoes a process in which the pressure (P) and volume (V) of the gas are PV^(-3) = is related as a constant. What will be the molar heat capacity of the gas for this process?
View SolutionMolar heat capacity of an ideal gas in the process = constant , is given by : . An ideal diatomic gas with occupies a volume at a pressure . The gas undergoes a process in which the pressure is proportional to the volume. At the end of the process the rms speed of the gas molecules has doubled from its initial value.
The molar heat capacity of the gas in the given process is :-
View SolutionMolar heat capacity of an ideal gas in the process = constant , is given by : . An ideal diatomic gas with occupies a volume at a pressure . The gas undergoes a process in which the pressure is proportional to the volume. At the end of the process the rms speed of the gas molecules has doubled from its initial value.
The molar heat capacity of the gas in the given process is :-
View Solution