In the circuit shown above the cells are ideal and of equal emfs the capacitance of the capacitor is C and the resistance of the resistor is R. X is first joined to Y and then to Z. After a long time the total heat produced in the resistor will be a equal to the energy finally stored in the capacitor b half the energy finally stored in the capacitor c twice the energy finally stored in the capacitor d four times the energy finally stored in the capacitor
Correct Answer is: d four times the energy finally stored in the capacitor The charge on the capacitor will change from -ℰC to +ℰC where ℰ = emf of each cell.∴ total charge flowing through the cell B is 2ℰC.∴ total energy supplied by B is 2ℰ2C.The energy finally stored in the capacitor is ℰ = 1/2 ℰ2C.∴ heat produced = 2ℰ2C = 4ℰ.
Related Solutions
In the circuit shown the cells are ideal and of equal emfs, the capacitance of the capacitor is C and the resistance of the resistor is R . X is first joined to Y and then to Z . After a long time, the total heat produced in the resistor will be
View SolutionIn the circuit shown the cells are ideal and of equal emfs, the capacitance of the capacitor is C and the resistance of the resistor is R . X is first joined to Y and then to Z . After a long time, the total heat produced in the resistor will be
View SolutionIn the circuit shown, the cell ideal and their emf are same. is the capacitance of the capacitor and the value of resistance is R. X is first added and then added to Z. The total heat produced in the resistance after a long time is:
View SolutionThe heat produced by a resistor in any time t during the charging of a capacitor in a series circuit is half the energy stored in the capacitor by that time. Current in the circuit is equal to the rate of increase in charge on the capacitor.
View SolutionWhen a charged capacitor is discharged through a resistor, heat is produced in the resistor
In charging a capacitor, energy is stored in the capacitor.
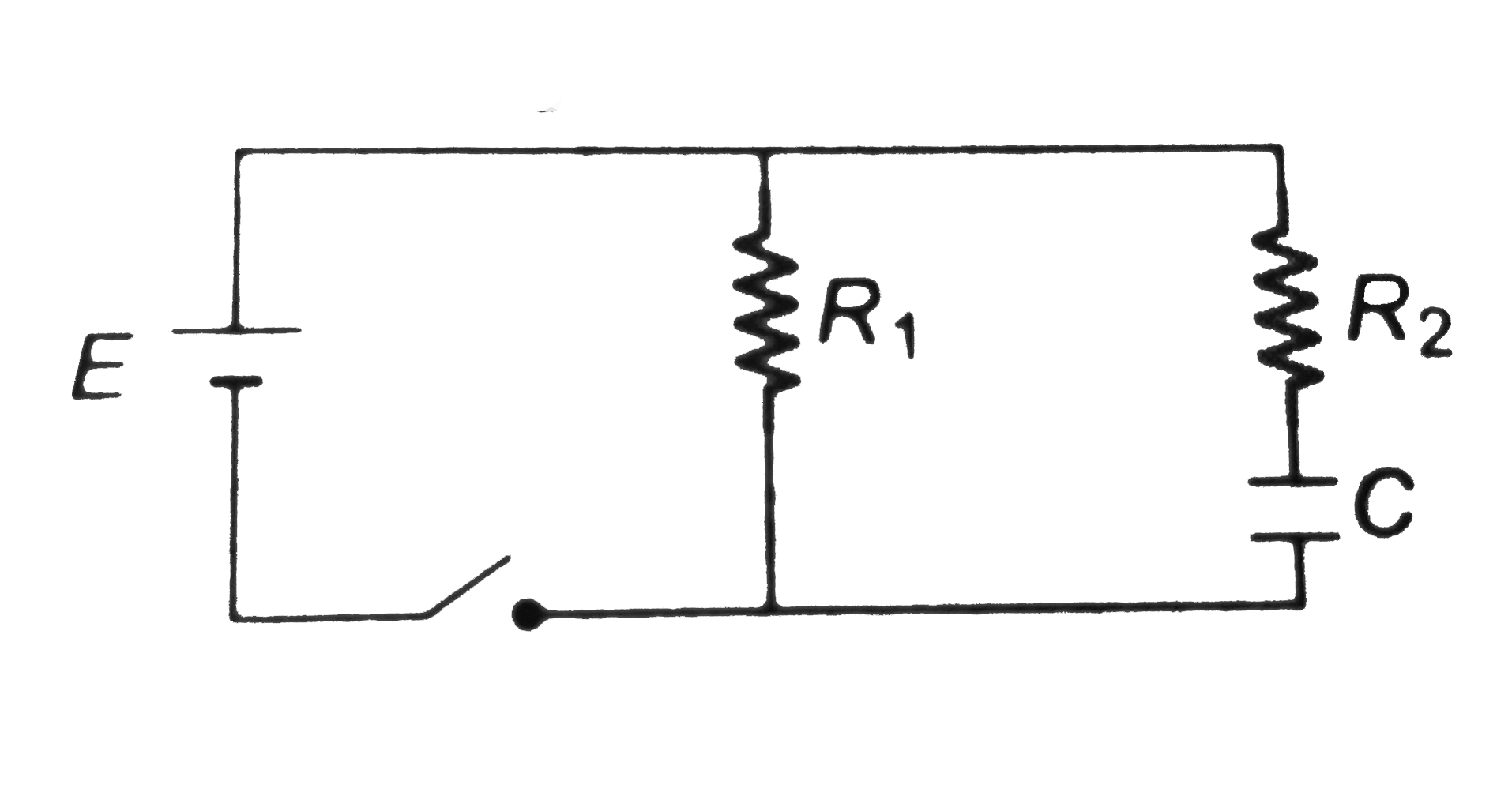
View SolutionFor the circuit shown in figure, find
(a) the initial current through each resistor
(b) steady state current through each resistor
(c) final energy stored in the capacitor
(d) time constant of the circuit when switch is opened.
View SolutionFor the circuit shown in figure, find
(a) the initial current through each resistor
(b) steady state current through each resistor
(c) final energy stored in the capacitor
(d) time constant of the circuit when switch is opened.

View SolutionA capacitor is charge until it stores an energy of 1J. A second uncharged capacitor is connected to it, so that charge districutes equally. The final energy stored in the second capacitor is
View SolutionA capacitor is charge until it stores an energy of 1J. A second uncharged capacitor is connected to it, so that charge districutes equally. The final energy stored in the second capacitor is
View SolutionIf an uncharged capacitor is charged by connecting it with an ideal battery and a resistance R as shown. Then heat generated in resistor R by the time capacitor stores energy is :

View SolutionIf an uncharged capacitor is charged by connecting it with an ideal battery and a resistance R as shown. Then heat generated in resistor R by the time capacitor stores energy (1)/(8) CV^(2) is :
View SolutionThe capacitor of capacitance C in the circuit shown in fully charged initially. Resistance is R.– After the switch S is closed, the time taken to reduce the stored energy in the capacitor to half its initial value is
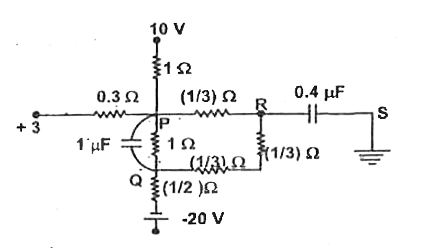
View SolutionShown in the figure is network of capacitors & resistors. The potentials of some of the nodes are given. Find the
(a) potential of
(b) energy stored in the capacitor connected between R&S
(c) energy stored in the capacitor connected between P&Q
View SolutionShown in the figure is network of capacitors & resistors. The potentials of some of the nodes are given. Find the
(a) potential of
(b) energy stored in the capacitor connected between R&S
(c) energy stored in the capacitor connected between P&Q

View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1/sqrt2q_"max" , where q_"max" is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1/sqrt2q_"max" , where q_"max" is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionBy evaluating ,show that when a capacitor is charged by connecting it to a battery through a resistor,the energy dissipated as heat equals the energy stored in the capacitor.
View SolutionBy evaluating ,show that when a capacitor is charged by connecting it to a battery through a resistor,the energy dissipated as heat equals the energy stored in the capacitor.
View SolutionBy evaluating ,show that when a capacitor is charged by connecting it to a battery through a resistor,the energy dissipated as heat equals the energy stored in the capacitor.
View SolutionA capacitor of capacitance C is charged by connecting it to a battery. The battery is now removed and this capacitor is connected to a second uncharged capacitor of capacitance C' . If the charge distributes equally on the two capacitors, the ratio of the total energy stored in the capacitors after connection to the total energy stored in them before connection is :
View Solution