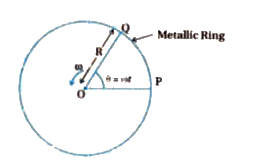
A metallic rod of length ‘l’ is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius r about an axis passing through the centre and perpendicular to the plane of the rinig. A constant uniform magnetic field B parallel to the axis is present every where. Using Lorentz force explain how emf is induced between the centre and the metallic ring and hence obtain the expression for it.
As the rod is rotated free electrons in the rod move towards the outer end due to Lorentz force and get distributed over the ring. Thus the resulting separation of charges produces an emf across the ends of the rod. At a certain value of emf there is no more flow of electrons and a steady state is reached. Expression for Induced emf in a Rotating Rod Consider a metallic rod OA of length l which is rotating with angular velocity w in a uniform magnetic field B the plane of rotation being perpendicular to the magnetic field. A rod may be supposed to be formed of a large number of small elements. Consider a small element of length dx at a distance x from centre. If v is the linear velocity of this element then area swept by the element per second =vdx The emf induced across the ends of element
Related Solutions
A metallic rod of length 'l' is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius r, about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present every where. Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtain the expression for it.
View SolutionA metallic rod of length 'I' is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circualr metallic ring of a radius r, about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present every where. Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtain the expression for it.
View SolutionA metallic rod of length is rotated with a frequency with one end hinged at the center and the other end at the circumference of a circular metallic ring of radius , about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field parallel to the axis is present everywhere . Using Lorentz force, explain how is induced between the centre and the metallic ring and hence obtained the expression for it.
View SolutionA metallic rod of length .L. is rotated with angular frequency of .omega. with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius R, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View SolutionA metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View SolutionA metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View SolutionA metallic rod of length 'I' is rotated with angular frequency of with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 'l', about an axis passing through its centre and perpendicular to the plane of ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View SolutionA metallic rod of length l is rotating with an angular frequency w with one end hinged at the centre and other end at the circumference of a circular metallic ring of radius l about an axis passing through the centre and perpendicular to the plane of rotation. A uniform magnetic field of B tesla is perpendicular to the plane of rotation everywhere. Find the emf between the centre of the metallic ring.
View SolutionA metallic rod of 1m length is rotated with a frequency of with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1m, about an axis passing through the centre and perpendicular to the plane of the ring (fig) A constant and uniform magnetic field of 1T parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring.

View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular to the plane of the ring as per figure. A constant and uniform magnetic field of 1T parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring ?
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular to the plane of the ring (Fig.). A constant and uniform magnetic field of 1 T parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring?
View SolutionA metallic rod of length l and resistance R is rotated with a frequency v, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius l, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere.
(a) Derive the expression for the induced emf and the current in the rod.
(b) Due to the presence of the current in the rod and of the magnetic field, find the expression for the magnitude and direction of the force acting on this rod.
(c) Hence obtain the expression for the power required to rotate the rod.
View SolutionA conducting rod of 1 m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field of 1 T parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring?
View SolutionA metallic rod of 1m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular me tallic ring of radius 1m, about an axis passing through the centre and perpendicular to the plane of the ring (see figure). A constant and uniform magnetic field of 1T parallel to the axis present everywhere. What is the emf between the centre and the metallic ring?
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 , with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 , with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 , with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
View SolutionA metallie rod of 1 m length is rotated with a frequency of 50 revis, with one end hinged at the centre and the other end at the eireumference of a circular metallic ring of radius 1m, about an axis passing through the centre and perpendicular to the plane of the ring as in figure. A constant and uniform magnetic field of the parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring?

View SolutionA 1.0 m long metallic rod is rotated with an angular frequency of 400 rad s^(-1) about an axis normal to the rod passing through its one end. The other end of the rod is in contact with a circular metallic ring. A constant and uniform magnetic field of 0.5 T parallel the centre and the ring.
View SolutionA metallic rod of length l and resistance R is rotated with a frequency v, with one end hinged at the center and the other end at the circumference of a circular metallic ring of radius l, about an axis passing through the centre and perpendicular to the palne of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere.
(i) Derive the expression for the induced emf and the current in the rod.
(ii) Due tot the presence of the current in the rod and of the magnetic field, find and expression for the magnitude and direction of the force acting on this rod.
(iii) Hence, obtain the expression for the power required to rotate the rod.
View Solution