The small sphere of mass m is attached to a string of length L and rests on the smooth surface of a fixed sphere of radius R. The center of the sphere is directly below the point where the string is attached. Obtain an equation for the tension in the string in terms of m L h and R.
From the geometry we haveThus the equilibrium equations can be written
Related Solutions
A small sphere of mass m is attached to a spring of spring-factor k, and normal length l. If the sphere rota with radius r at frequency u, then tension in the spring is ·

View SolutionA uniform sphere of weight w and radius 3 m is suspended by a string of length 2 m and attached to a frictionless wall, as shown in the figure. there will be tension in the string
View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R . The ratio of tensions in both the strings is
View SolutionA small metallic sphere of mass m is suspended from the ceiling of a car accelerating on a horizontal road with constant acceleration a. The tension in the string attached with metallic sphere is
View SolutionA small metallic sphere of mass m is suspended from the ceiling of a car accelerating on a horizontal road with constant acceleration a. The tension in the string attached with metallic sphere is
View SolutionA sphere of mass 0.1kg is attached to an inextensible string of length 1.3m whose upper end is fixed to the ceilling The sphere is made to describe a horizontal circle of radius 0.5m Calculate time period of revolution and tension in the string .
View SolutionA chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
View SolutionA mass m attached to a string of length 'l' is suspended from the ceiling and is set into motion in a horizontal circle of radius 'r and the string making an angle with the vertical. If , is the breaking tension of the string the maximum value of ris :
View SolutionTwo spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio of their tension:
View SolutionA small spehre of mass is connected by a stirng to a nail at and moves in a circle of radius on the smooth plane inclined at an angle with the horizontal. If the sphere has a velocity at the top position A. Mark the correct options.
1)the tension in the string as the sphere passes the 90∘ position B is equal to m( u^2/l − 2gsinθ )
2)the tension in the string at the bottom most position C is equal to
m( u^2/l + 5gsinθ )
3)the tension in the string as the sphere passes the 90∘ position B is equal to m( u^2/l + 2gsinθ )
4)the tension in the string at the bottom most position C is equal to
m( u^2/l − 5gsinθ )

View SolutionA block of mass is attached to a string of length . The block is released when the string is horizontal , it picks up a particle of kept at rest at the lowest point. The maximum height attached by the combined mass is
View SolutionTwo identical small charged spheres, each having a mass m, hang in equilibrium the length of each string is l, and the angle made by any string with the vertical is theta . Find the magnitude of the charge on each sphere.
View SolutionA bullet of mass m is moving with a horizontal theta at an angle 50 "m s"^(-1) fired with a velocity of At the highest point of its trajectory, it makes a head-on collision with a sphere attached to a massless string of length l and slams into a sphere of mass 3m. After the collision, the string 120^@ moves at an angle of angle theta What is ?
View SolutionA sphere of radius 25 cm and mass 1 kg is hung by a string of negligible mass and length 40 cm, then tension in the string is -
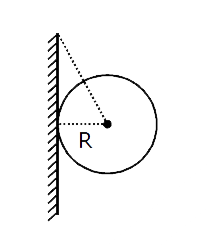
View SolutionA partical of mass m is attached to a massless string of length l and is oscillating in a vrtical plane with the other end of the string fixed to a rigid support. The tension in the string at a certain instant is T=kmg .
View SolutionA sphere of mass 100 g is attached to a string of length 1.3 m whose upper end is fixed to ceilings. The sphere is made to describe a horizontal circle of radius 50 cm. The time period of the revolution is :
View SolutionTwo masses are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
View SolutionThe masses (M+m) and (M-m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are relased from rest the acceleraion of the system is .
View Solution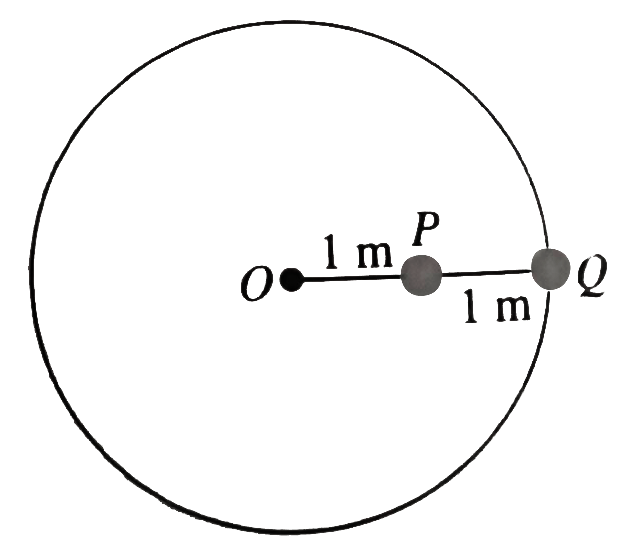
Two spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio:
View Solution