Develop the notions of work and kinetic energy and show that it leads to work energy theorem.The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5m what is the speed with which the bob arrives at the lowermost point given that it dissipated 5% of its initial energy against air resistance?
Statement : The change in kinetic energy of a particle is equal to the work done on it by the net force. i.e. kf – ki = WProof : Consider a particle of mass m is moving with initial speed u to final speed v. Let a be its constant acceleration and S be its distance traversed. The kinematic relation is given byv2 – u2 = 2as –––– 1Multiplying bothsides by m/2 we have1/2mv2 – 1/2mu2 = mas = FS –––– 2Where the last step follows from Newtons second law.We can generalise Equation 1 to three dimensions by employingvectors v2 – u2 = 2a.dOnce again multiplying both sides by m/2 we obtain1/2mv2 – 1/2mu2 = m vectora.d = vectorF.d–––– 3The above equation provides a motivation for the definitions of work and kinetec energy.In equation 3 1/2mv2 – 1/2mu2 = kf – ki Where ki kf are initial and final kinetic energies and vectorF.d = W where W refers work done by a force on the body over a certain displacement. kf – ki = W ––––– 4Equation 4 is also a special case of the work–energy WE theorem.Problem : Here h = 1.5m V = ? Energy dissipated = 5% Taking B as the lowest position of the bob its potential energy at B is zero. At the horizontal position A total potential energy of the bob is mgh.In going from A to B P.E of the bob is converted into K.EEnergy conserved = 95% mghIf V is velocity acquired at B then K.E = 1/2mv2 = 95/100mgh
Related Solutions
The bob of a pendulum is released from a horizontal position. If the length of the pendulum is , what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is , what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance ?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m what is the speed with which the bob arrives at the lowermost point , given that it dissipated 5% of its initial energy against air resistance ?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance ?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance ?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5m, what is the speed with which the bob arrive at the lower most point, given that, it dissipated 5% of its initial energy against air resistance?
View SolutionThe bob A of a simple pendulum is released from a horizontal position A as shownin in figure. If the length of the pendulum is 1.5m , what is the speed with which the bob arrives at the lowermost point B, given that it dissipates of its initial energy against air resistance ?
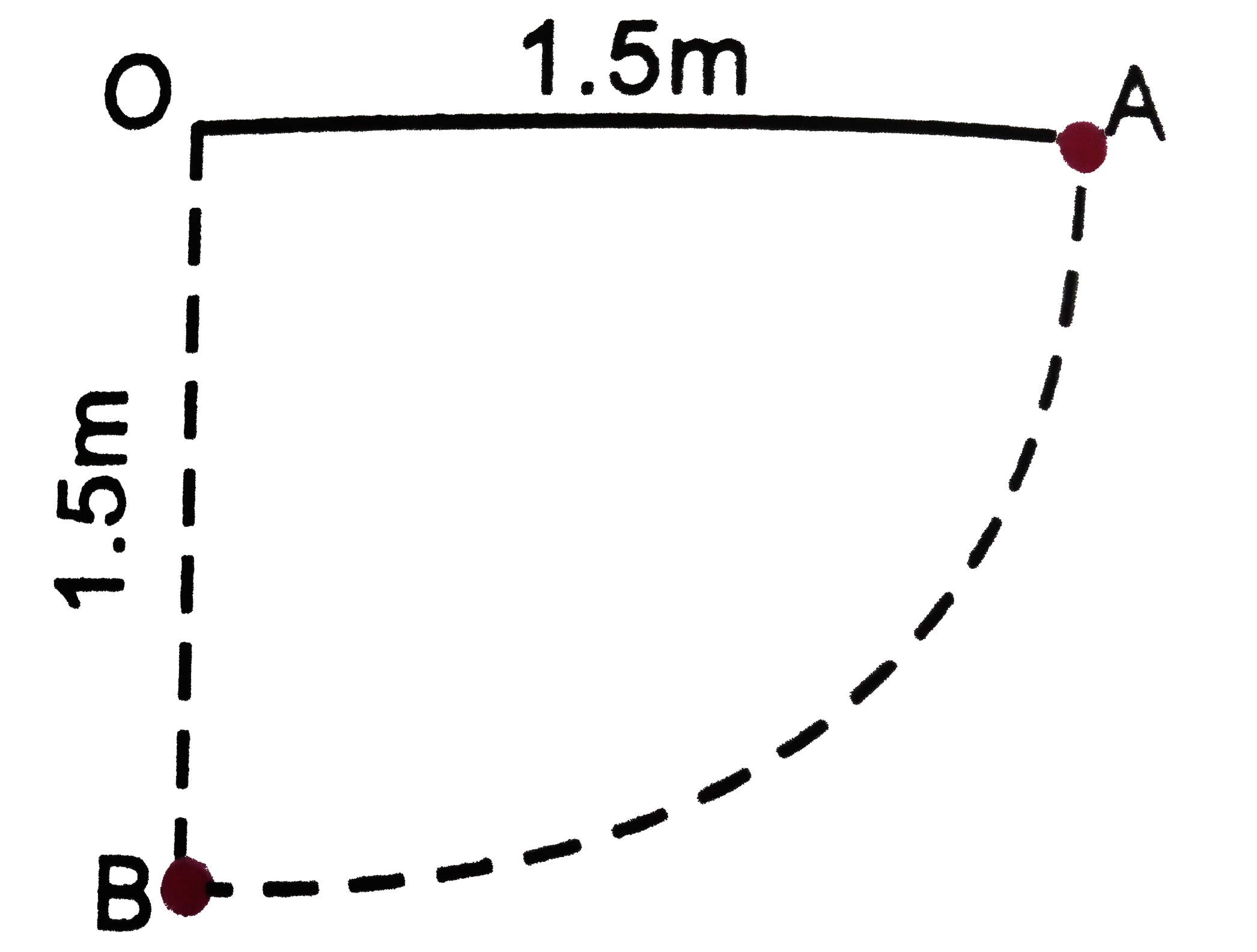
View SolutionThe bob A of a simple pendulum is released from a horizontal position A as shownin in figure. If the length of the pendulum is 1.5m , what is the speed with which the bob arrives at the lowermost point B, given that it dissipates 5% of its initial energy against air resistance ?
View SolutionThe bQB of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bQB arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?
View SolutionThe bob of pendulum is released from a horizontal position . If the length of the pendulum is 1.5 m ,what is the speed with which the bob arrives at the speed with which the bob arrives at the lowermost point , given that it dissipated 5 % of its intial energy against air resistance ?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1 m, what is the speed with which the bob reaches the lower most point, given that it dissipates 10% of the initial energy against air resistance ?
View SolutionChoose the most appropriate option.
The bob of a pendulum is released from a horizontal position A as shown in the figure. If the length of the pendulumis 1.5 m, what is the speed with which the bob arrives at the lower most point B, given that it dissipated 5% of its initial energy against air resistance?
View Solutionकिसी लोलक के गोलक को क्षैतिज अवस्था से छोड़ा गया है । यदि लोलक की लम्बाई है तो निम्नतम बिंदु पर आने पर गोलक की चाल क्या होगी ? यह दिया गया है कि इसकी आरम्भिक ऊर्जा का अंश वायु प्रतिरोध के विरुद्ध क्षय हो जाता है।
View SolutionThe bob of a pendulum is released from a horizontal position A as shown in the figure. If the length of the pendulum is 1.5 m, what is the speed with which the pendulum comes to the lowest point B, given that it dissipates 5% of its initial energy against air resistance?
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of pendulum is 2 m, what is the speed with which the bob arrives at the lower most point. Assume that 10% of its energy is dissipated against air resistance.
(Take )
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of pendulum is 2 m, what is the speed with which the bob arrives at the lower most point. Assume that 10% of its energy is dissipated against air resistance. (Take g = 10 m s^(-2) )
View Solution