Find the angle between two diagonals of a cube.
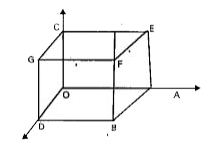
Let O one of the vertices of the cube taken as origin and the three sides OA OB OC are taken as Co-ordinate axes. Let OA = OB = OC = a the four diagonals are vectorOF AG DE and BC The Co-ordinates of the vertices of the cube are O0 0 0 Aa 0 0 B0 a 0 C0 0 a Fa a 0 Da a 0 Ea 0 a G0 a a D.Rs of OF are a – 0 a – 0 a – 0 = a a a D.Rs of AG are 0 – a a – 0 a – 0 = –a a a If O is the angle between the diagonals OF and AGthen Similarly the angle between any pair of diagonals can be shown to be cos–1 1/3.
Related Solutions
Find the angle between any two diagonals of a cube.
View SolutionFind the angle between any two diagonals of a cube.
View SolutionFind the angle between the diagonals of a cube .
View SolutionFind the angle between any two diagonals of a cube.
View Solutionएक घन के किन्ही दो विकर्णों के मध्य कोण ज्ञात कीजिए ।
View SolutionFind the angle between any two diagonals of a cube.
View SolutionFind the angle between any two diagonals of a cube.
View SolutionIn a unit cube. Find The angle between a diagonal of a cube and the diagonal of a face of the cube
View SolutionThe angle between the two diagonals of a cube is .....
View SolutionThe angle between the two diagonals of cube is
View SolutionThe angle between the two diagonals of cube is
View SolutionThe angle between two diagonals of a cube is
View SolutionThe angle between two diagonals of a cube is
View SolutionThe angle between two diagonals of a cube İs
View Solutionघन के किन्हीं दो विकर्णों के बीच का कोण होगा :
View SolutionThe angle between the two diagonals of a cube is .....
View SolutionThe angle between two diagonals of a cube will be
View SolutionThe angle between two diagonals of a cube will be
View SolutionFind the angle between the diagonals of a cube .

View SolutionThe angle between a diagonal of a cube and the diagonal of a face of the cube is
View Solution