The bob of a pendulum is released from a horizontal position. If the length of pendulum is 2 m, what is the speed with which the bob arrives at the lower most point. Assume that 10% of its energy is dissipated against air resistance.
(Take g=10ms−2)
4ms−1
6ms−1
8ms−1
10ms−1
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Determine the potential energy at the starting position (A)
The bob of the pendulum is released from a horizontal position, which means it is at a height equal to the length of the pendulum when it is at point A.
- Given:
- Length of the pendulum (L) = 2 m
- Mass of the bob (m) = m (we will keep it as a variable)
- Acceleration due to gravity (g) = 10 m/s²
The potential energy (PE) at point A is given by the formula:
PE=mgh
Where:
- h=L=2m
Thus,
PEA=mg⋅2=2mg
Step 2: Calculate the total mechanical energy at point A
At point A, the bob is at rest, so its kinetic energy (KE) is 0. Therefore, the total mechanical energy (E) at point A is:
EA=PEA+KEA=2mg+0=2mg
Step 3: Determine the energy at the lowest point (B)
At point B (the lowest point), the potential energy is zero because the height is 0. However, we need to account for the energy lost due to air resistance. The problem states that 10% of the energy is dissipated.
Thus, the energy remaining at point B is:
EB=90% of EA=0.9×2mg=1.8mg
Step 4: Relate the remaining energy to kinetic energy at point B
At point B, all the remaining energy is converted into kinetic energy:
KEB=12mv2
Setting the kinetic energy equal to the remaining energy:
12mv2=1.8mg
Step 5: Solve for the speed (v)
We can cancel the mass (m) from both sides of the equation:
12v2=1.8g
Substituting g=10m/s2:
12v2=1.8×10
12v2=18
Multiplying both sides by 2:
v2=36
Taking the square root of both sides:
v=6m/s
Conclusion
The speed with which the bob arrives at the lowermost point is 6 m/s.
---
The bob of the pendulum is released from a horizontal position, which means it is at a height equal to the length of the pendulum when it is at point A.
- Length of the pendulum (L) = 2 m
- Mass of the bob (m) = m (we will keep it as a variable)
- Acceleration due to gravity (g) = 10 m/s²
PE=mgh
Where:
- h=L=2m
PEA=mg⋅2=2mg
At point A, the bob is at rest, so its kinetic energy (KE) is 0. Therefore, the total mechanical energy (E) at point A is:
EA=PEA+KEA=2mg+0=2mg
At point B (the lowest point), the potential energy is zero because the height is 0. However, we need to account for the energy lost due to air resistance. The problem states that 10% of the energy is dissipated.
EB=90% of EA=0.9×2mg=1.8mg
At point B, all the remaining energy is converted into kinetic energy:
KEB=12mv2
12mv2=1.8mg
We can cancel the mass (m) from both sides of the equation:
12v2=1.8g
12v2=1.8×10
12v2=18
v2=36
v=6m/s
The speed with which the bob arrives at the lowermost point is 6 m/s.
Topper's Solved these Questions
- WORK , ENERGY AND POWERBook:NCERT FINGERTPS ENGLISHChapter:WORK , ENERGY AND POWERExercise:NCERT
Explore 18 Videos
- WORK , ENERGY AND POWERBook:NCERT FINGERTPS ENGLISHChapter:WORK , ENERGY AND POWERExercise:ASSERTION & REASON
Explore 15 Videos
- WAVESBook:NCERT FINGERTPS ENGLISHChapter:WAVESExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
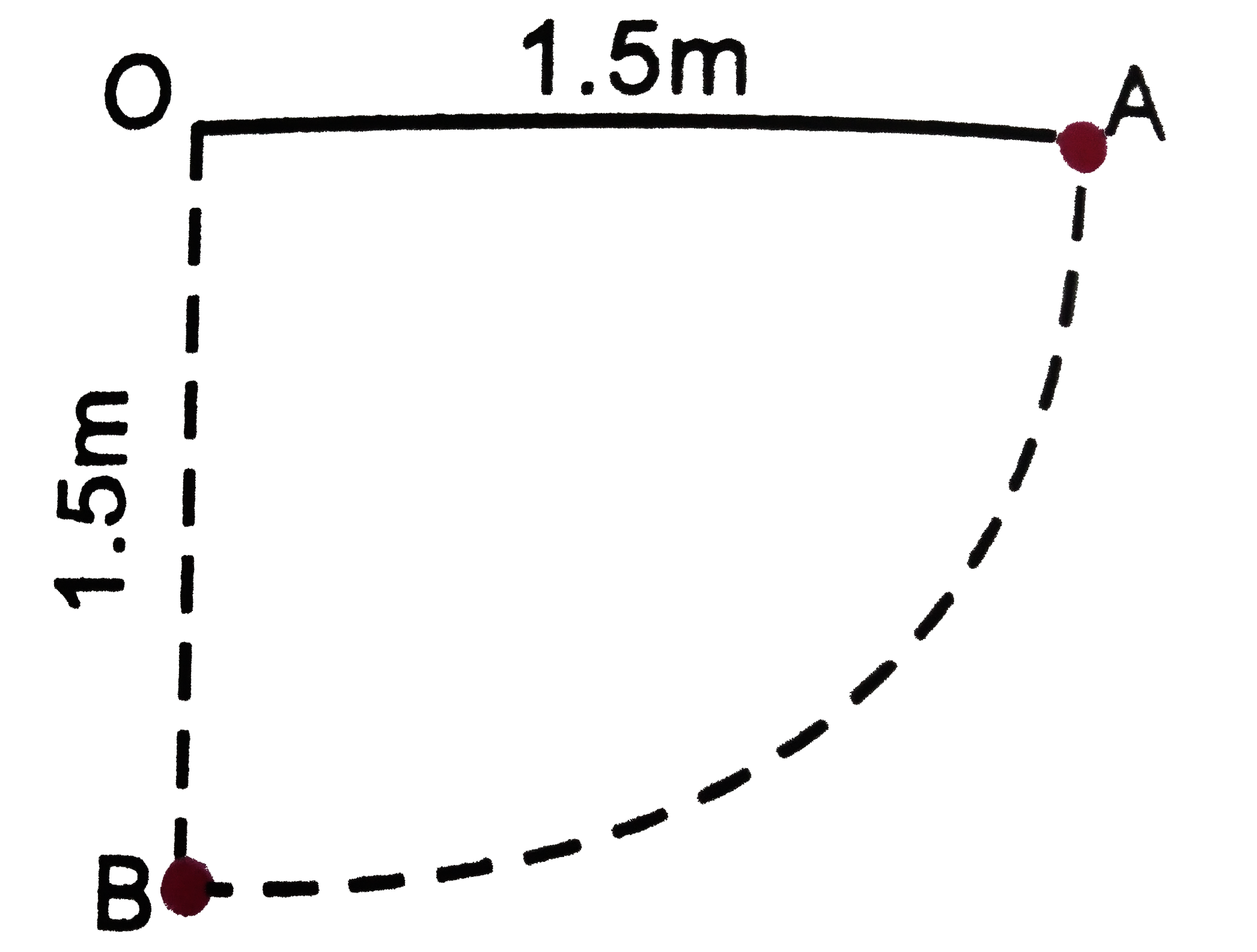
The bob A of a simple pendulum is released from a horizontal position A as shownin in figure. If the length of the pendulum is 1.5m , what is the speed with which the bob arrives at the lowermost point B, given that it dissipates 5% of its initial energy against air resistance ?
View SolutionA pendulum bob on a 2 m string is displaced 60∘ from the vertical and then released. What is the speed of the bob as it passes through the lowest point in its path
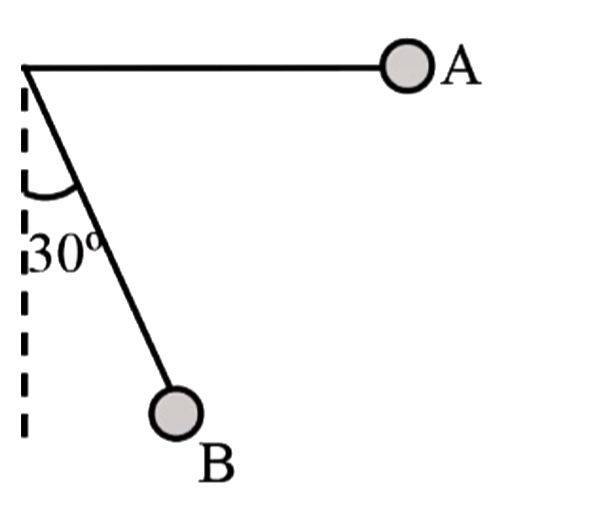
View SolutionA simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
View SolutionA pendulum of length 2 m lift at P . When it reaches Q , it losses 10% of its total energy due to air resistance. The velocity at Q is

View SolutionThe bob of a simple pendulum is imparted a velocity of 5 ms−1 when it is at its mean position.To what maximum vertical height will it rise on reaching at its extreme position if 60% of its energy is lost on overcoming the friction of air?
(Take g=10 m s−2)
View SolutionThe bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with the upward vertical.
View SolutionA pendulum bob has a speed of 3ms−1 at its lowest position. The pendulum is 0.5 m long. The speed of the bob, when string makes an angle of 60∘ to the vertical is (take, g=10ms−1)
View SolutionIt takes 0.2 s for a pendulum bob to move from the mean position to one end. What is the time period of the pendulum?
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionThe bob of a simple pendulum of length l dropped from a horizontal position strikes a block of the same mass elastically, placed on a horizontal table (frictionless) as shown in the diagram, the block shall have kinetic energy-

View Solution

