An I section has the following dimensions Top flange = 8 cm × 2 cm; Bottom flange = 12 cm × 2 cm; Web = 12 cm × 2 cm; Over all depth of the section = 16 cm. Determine the MI of the I section about two centroidal axis.
Since diagram is symmetrical about y axis i.e. X = 0 x1 = x2 = 0 A1 = 8 × 2 = 16 cm2 A2 = 12 × 2 = 24 cm2 A3 = 12 × 2 = 24 cm2 y1 = 2 + 12 + 2/2 = 15 cm y2 = 2 + 12/2 = 8 cm y2 = 2/2 = 1 cmY = A1 y1 + A2y2 + A3y3/A1 + A2 + A3 = 16 × 15 + 24 × 8 + 24 × 1/16 + 24 + 24 = 7.125cm C.G. = 0 7.125 Moment of inertia M.I. about x-x axis = IXX = IXX1 + IXX2 IXX1 = IGXX1 + A1h12 = bd3/121 + A1Y – y12 = 8 × 23/12 + 16 7.125 – 152 = 997.58 cm4 ...i IXX2 = IGXX2 + A2h22 = bd3/122 + A2Y – y22 = 2 × 123/12 + 24 7.125 – 82 = 306.375 cm4 ...iiIXX3 = IGXX3 + A3h32 = bd3/123 + A2Y – y32 = 12 × 23/12 + 24 7.125 – 12 = 908.375 cm4 ...iii IXX = IXX1 + IXX2+ IXX3 = 997.58 + 306.375 + 908.375 = 2212.33 cm4 ...ivMoment of inertia M.I. about y-y axis = Iyy = Iyy1 + Iyy2; h = 0 Since X = 0 i.e.; X1 = X2 = 0 Iyy = Iyy1 + Iyy2+ Iyy3 = db3/121 + db3/122 + db3/123 = 2 × 83/12 + 12 × 23/12 + 2 × 123/12 = 381.33 cm4 ...iv IXX = 2212.33 cm4; Iyy = 381.33 cm4
Related Solutions
A tube 1 cm^2 in cross = section is attached to the top of a vessel 1 cm high and of cross - section 100 cm^2 Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in fig. Take g = ms^I(-2) Now.
View SolutionDiagram of the Adjacent picture frame has outer dimensions = and inner dimensions .Find the area of each section of the frame,if the width of each section is same.
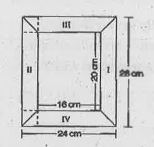
View SolutionDiagram of the adjacent picture frame has outer dimensions and inner dimensions .Find the area of each section of the frame ,if the width of each section is same.
View SolutionDiagram of the adjacent picture frame has outer dimensions
View SolutionDiagram of the adjacent picture frame has outer dimensions = 24 cm 28 cm and inner dimensions 16 cm 20 cm. Find the area of each section of the frame, if the width of each section is same.
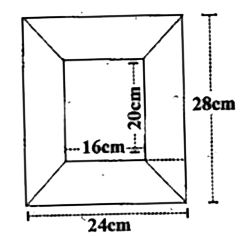
View SolutionA tube in cross- section is attached to the top of a vessel 1 cm high and of cross - section 100 Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in fig. Take g =10 .

View SolutionA tube in cross- section is attached to the top of a vessel 1 cm high and of cross - section 100 Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in fig. Take g =10 .

View SolutionA pipe of varying area of cross-section is held such that its axis is horizontal. At two cross sections A and B, its radii are 8 cm and 4 cm. If velocity of water at A through the pipe is 16 cm and pressure at A is dyne/ , find the pressure at cross-section B.
View SolutionA pipe of varying area of cross-section is held such that its axis is horizontal. At two cross sections A and B, its radii are 8 cm and 4 cm. If velocity of water at A through the pipe is 16 cm s^(-1) and pressure at A is 10^( -6) dyne/ cm^(2) , find the pressure at cross-section B.
View SolutionIn the given cross-section: CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm The perimeter of the trapezium part of the cross section, is
View SolutionIn the given cross-section: CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm The area of the semi- circular part of the cross section, is
View SolutionIn the given cross-section: CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm The perimeter of the rectangular part of the cross section, is
View SolutionIn the given cross-section: CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm The perimeter of the cross section, is
View SolutionIn the given cross-section: CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm The area of the cross section, is
View SolutionThe figure shows the cross-section of the interior of thermos flask .
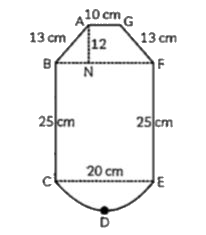
The top part is a trapezium , the middle part is a rectangle and the bottom part is a semicircle if CE = 20 cm , BC = 25 cm , AB = GF = 13 cm , AG = 10 cm and AN = 12 cm , the find :
The perimeter of the cross-section
View SolutionThe radii of the two ends of the cross section of a cone of height cm cm r_1 Cm and r_2 Cm. The volume of the cross section of a cone સેમી^(3) In
View Solution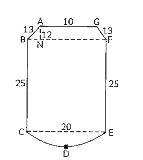
The dimension of various parts are:
CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm
The perimeter of the semi-circular part of the cross section, is
View SolutionDiagram of the adjacent picture frame has outer dimensions 28 cm xx 24 cm and inner dimensions 20 cm xx 16 cm . Find the area of shaded part of frame, if width of each section is the same.
View SolutionA parallelogram has sides of 12 cm and 8 cm. If the distance between the 12 cm sides is 5 cm, find the distance between 8 cm sides.
View Solutionएक मेज़ की ऊपरी सतह की विमाएँ मी सेमी और मी सेमी है। मेज़ की ऊपरी सतह का परिमाप होगा :
View Solution