A pipe of varying area of cross-section is held such that its axis is horizontal. At two cross sections A and B, its radii are 8 cm and 4 cm. If velocity of water at A through the pipe is 16 cm s−1 and pressure at A is 106 dyne/cm2 , find the pressure at cross-section B.
To find the pressure at cross-section B of a pipe with varying cross-section, we can apply the principles of fluid dynamics, specifically the continuity equation and Bernoulli's theorem. Here’s a step-by-step solution:
Step 1: Determine the Areas of Cross Sections A and B
Given the radii:
- Radius at A, rA=8cm
- Radius at B, rB=4cm
The area of a circle is given by the formula:
A=πr2
Calculating the areas:
- Area at A:
AA=π(8cm)2=64πcm2
- Area at B:
AB=π(4cm)2=16πcm2
Step 2: Use the Continuity Equation
The continuity equation states that the product of the cross-sectional area and the velocity of the fluid must be constant along the flow:
AA⋅VA=AB⋅VB
Where:
- VA=16cm/s (velocity at A)
- VB is the unknown velocity at B.
Rearranging the equation to solve for VB:
VB=AA⋅VAAB
Substituting the values:
VB=(64π)⋅(16)16π=64⋅1616=64cm/s
Step 3: Apply Bernoulli's Theorem
Bernoulli's theorem states:
PA+12ρV2A+ρghA=PB+12ρV2B+ρghB
Since the pipe is horizontal, the heights hA and hB are equal, thus the gravitational potential energy terms cancel out. We can simplify to:
PA+12ρV2A=PB+12ρV2B
Rearranging gives us:
PB=PA+12ρV2A−12ρV2B
Step 4: Substitute Known Values
Given:
- PA=106dyne/cm2
- VA=16cm/s
- VB=64cm/s
- Density of water ρ=1g/cm3=1000kg/m3=1000dyne/cm3
Substituting into the equation:
PB=106+12(1000)(16)2−12(1000)(64)2
Calculating the kinetic energy terms:
=106+8000−2048000
=106−2040000+8000
=106−2040000+8000=998080dyne/cm2
Final Answer
Thus, the pressure at cross-section B is:
PB=998080dyne/cm2≈99.808×104dyne/cm2
Given the radii:
- Radius at A, rA=8cm
- Radius at B, rB=4cm
A=πr2
Calculating the areas:
- Area at A:
AA=π(8cm)2=64πcm2
- Area at B:
AB=π(4cm)2=16πcm2
The continuity equation states that the product of the cross-sectional area and the velocity of the fluid must be constant along the flow:
AA⋅VA=AB⋅VB
Where:
- VA=16cm/s (velocity at A)
- VB is the unknown velocity at B.
VB=AA⋅VAAB
Substituting the values:
VB=(64π)⋅(16)16π=64⋅1616=64cm/s
Bernoulli's theorem states:
PA+12ρV2A+ρghA=PB+12ρV2B+ρghB
Since the pipe is horizontal, the heights hA and hB are equal, thus the gravitational potential energy terms cancel out. We can simplify to:
PA+12ρV2A=PB+12ρV2B
Rearranging gives us:
PB=PA+12ρV2A−12ρV2B
Given:
- PA=106dyne/cm2
- VA=16cm/s
- VB=64cm/s
- Density of water ρ=1g/cm3=1000kg/m3=1000dyne/cm3
PB=106+12(1000)(16)2−12(1000)(64)2
Calculating the kinetic energy terms:
=106+8000−2048000
=106−2040000+8000
=106−2040000+8000=998080dyne/cm2
Thus, the pressure at cross-section B is:
PB=998080dyne/cm2≈99.808×104dyne/cm2
Similar Questions
Water flows through a horizontal pipe of varying area of cross-section at the rate 5 cubic metre per minute. What is the velocity of water at a point where pipe radius is 10 cm?
View SolutionWater flows through a horizontal pipe of varying area of cross-section at the rate 5 cubic metre per minute. What is the velocity of water at a point where pipe radius is 10 cm?
View SolutionA horizontal pipe of varying cross-sectional area carries water flowing at a constant rate. The pressure at sections (1) and (2) are 50cm and 20cm of Hg. If the velocity of section (1) is 5m/s, what is the velocity of section (2). Also determine the ratio of areas at sections (1) and (2) (as shown in Fig.
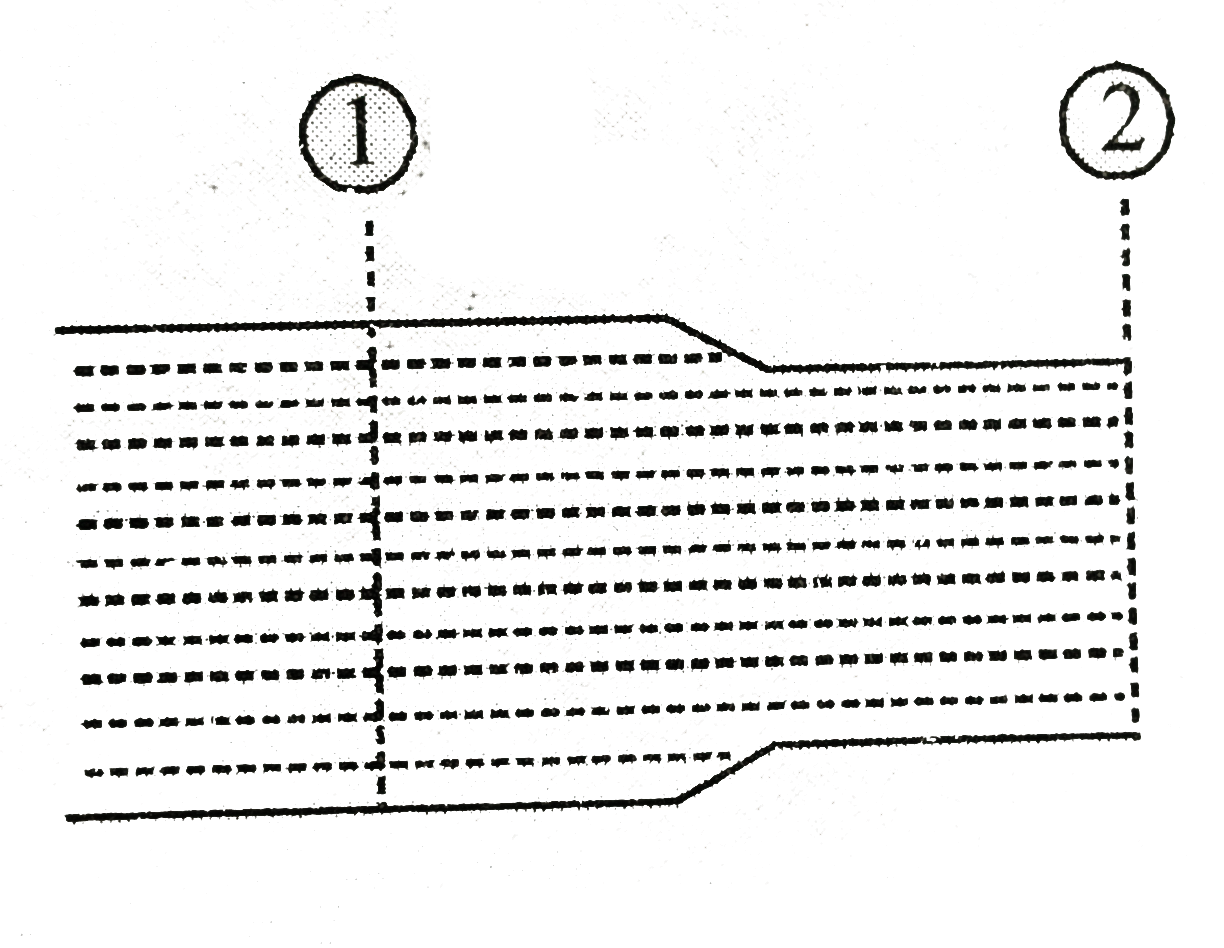
View SolutionA horizontal pipe of area of cross-section a and 3a respectively, then the ratio of velocity of flow at two different cross-section (If flow is streamline) is
View SolutionA pipe of constant cross - section is bent in a horizontal plane as shown in the figure . Points A and B are located on two different streamlines . Then
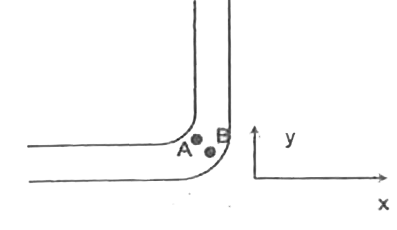
View SolutionThe cross-sectionss of a pipe at two points A and B are in the ratio 1.4. If the speed of water flowing through the pipe at point A is v, its speed at point B is
View SolutionWater flows along horizontal pipe whose cross-section is not constant. The pressure is 1 cm of Hg, where the velocity is 35 cm/s . At a point where the velocity is 65cm/s then pressure will be
View SolutionA lawn sprinkler has 20 holes, each of cross-sectional area 2.0x10−2cm2, and is connected to a hose pipe of cross sectional area 2.4cm2. If the speed of water in the hose pipe is 1.5ms−1, the speed of water as it emerges from the holes is
View SolutionWater flows along horizontal pipe whose cross-section is not constant. The pressureis 1 cam of Hg, where the veloecity is 35 cm/s . At a point where the velocity is 65cm/s then pressure will be
View SolutionA pipe of non uniform cross section has two distinct section 1 and 2 with areas 2cm2 and 4cm2 respectively. If the velocity of flowing liquid at section 1 is 5cm/s, determine the velocity at section 2.
View Solution
