A magnetic circuit made of mild steel is arranged as shown in Fig. . The central limb is wound with 500 turns and has a cross-sectional area of 800 mm2 . Each of the outer limbs has a cross-sectional area of 500 mm2 . The air-gap has a length of 1 mm. Calculate the current rquired to set up a flux of 1.3 mWb in the central limb assuming no magnetic leakage and fringing. Mild steel required 3800 AT/m to produce flux density of 1.625 T and 850 AT/m to produce flux density of 1.3 T
Flux in the central limb is = 1.3 mWb = 1.3 × 10−3 Wb Cross section A = 800 mm2 =800 × 10−6 m2 ∴ B = Φ/A = 1.3 × 10−6 /800 × 10−6 = 1.625 TCorresponding value of H for this flux density is given as 3800 AT/m.Since the length of the central limb is 120 mm. m.m.f. required is = H× l = 3800 × 120 × 10−3 = 456 AT/m. Air-gapFlux density in the air-gap is the same as that in the central limb. H = B/μ0 = 1.625/4π × 10−7 = 0.1293 × 10−7 AT/m Length of the air-gap = 1 mm = 10−3 m m.m.f. reqd. for the air-gap = H × l = 0.1293 × 107 × 10−3 = 1293 AT.The flux of the central limb divides equally at point A in figure along the two parallel path ABCD and AFED. We may consider either path say ABCD and calculate the m.m.f. required for it. The same m.m.f. will also send the flux through the other parallel path AFED. Flux through ABCD = 1.3 × 10−3 /2 = 0.65 × 10−3 Wb Flux density B = 0.65 × 10−3 /500 × 10−6 = 1.3 T The corresponding value of H for this value of B is given at 850 AT/m. ∴ m.m.f. reqd. for path ABCD = H × l = 850 × 300 × 10−3 = 255 AT As said above this m.m.f. will also send the flux in the parallel path AFED. Total m.m.f. reqd. = 456 + 1293 + 255 = 2004 AT Since the number of turns is 500 I = 2004/500 = 4A
Related Solutions
If cross- sectional area of limb I is and that of limb II is then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
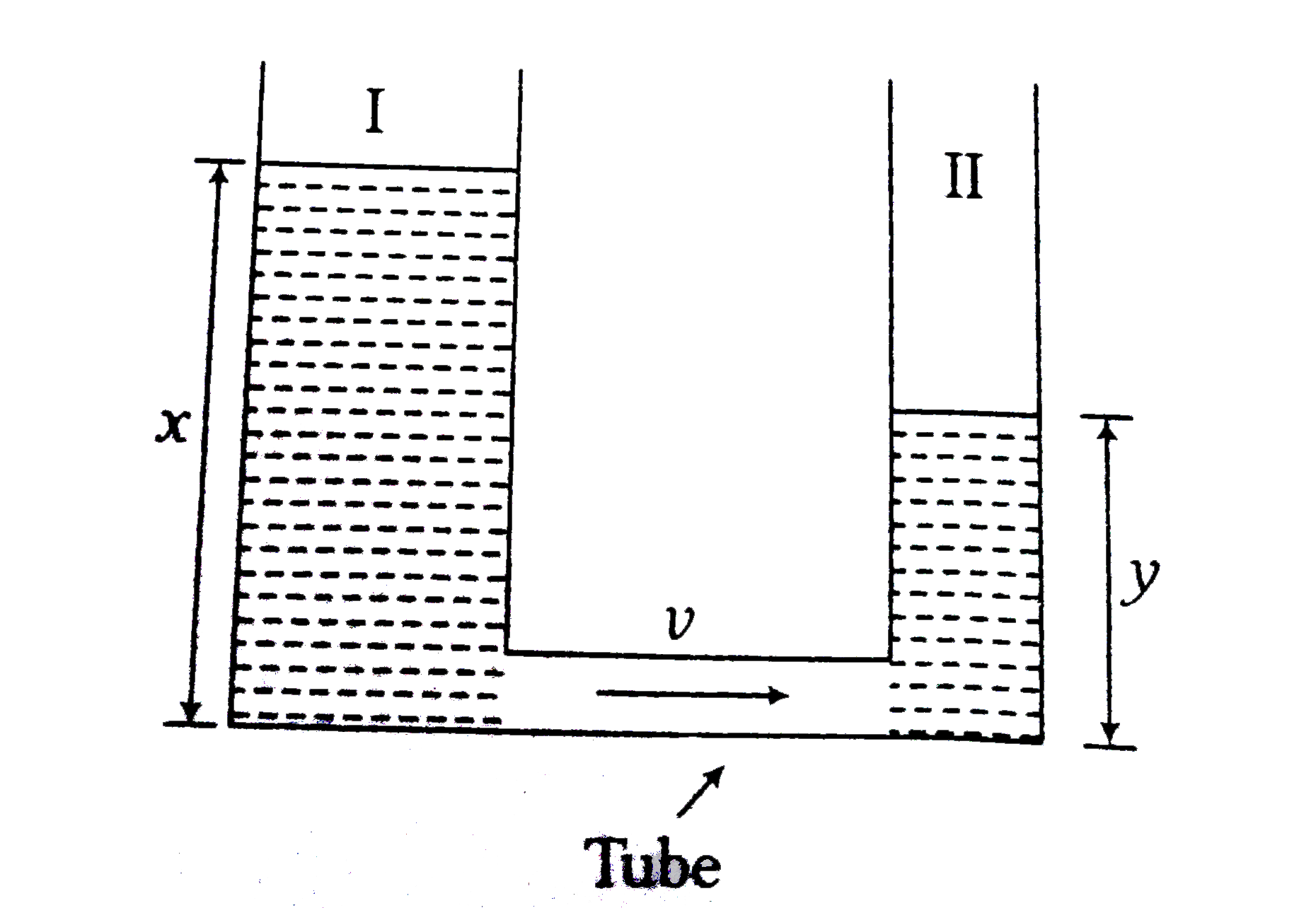
View SolutionIf cross- sectional area of limb I is and that of limb II is then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
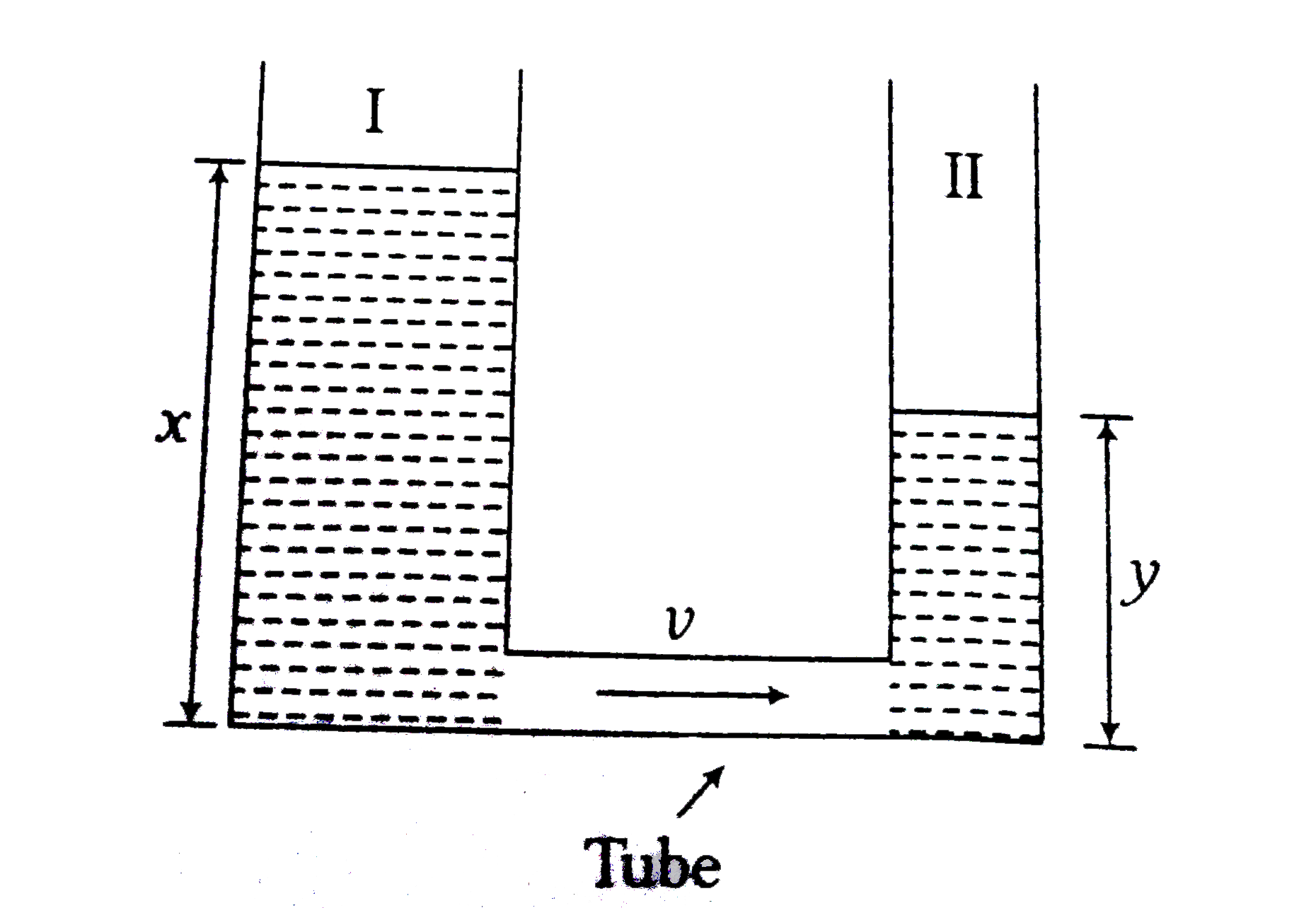
View SolutionA U-tube is almost half-filled with mercury. The wider limb has an area of cross-section of 2cm^(2) , and the cross-section of the narrow limb is 1cm^(2) . If 52cm^(3) of water is poured into the wider limb, then what will be the depression of the mercury level in that limb? The density of mercury = 13.6g*cm^(-3) .
View SolutionIn a hydraulic press , the narrower limb has an area of cross - section while that on the liquid in the narrower limb to a lift a vehicle of vehicle of 1000 kg kept on top of the fluid in the larger limb of cross section '1 m^2' ?
View SolutionAn ideal liquid of density rho is pushed with velocity v through the central limb of the tube shown in fig. What force does the liquid exert on the tube? The cross sectional areas of the three limbs are equal to A each. Assume stream-line flow.
View SolutionAn ideal liquid of density rho is pushed with velocity v through the central limb of the tube shown in fig. What force does the liquid exert on the tube? The cross sectional areas of the three limbs are equal to A each. Assume stream-line flow.
View SolutionFig, shows a U-tube of uniform cross-sectional area A accelerated with acceleration a as shown. If d is the seperation between the limbs. Then the difference in the levels of the liquid in the U-tube is
View SolutionCalculate the electrical conductivity of the material of a conductor of length 3m, area of cross section 0.2 having a resistance of 2 ohm.
View SolutionA solenoid has 2000 turns wound over a length of 0.3 m . Its cross-sectional area is equal to 1.2 xx 10^(-3) m^(2) . Around its central cross-section a coil of 300 turns in wound. If an initial current of 2 A flowing in the solenoid is reversed in 0.25 s , the emf induced in the coil is
View SolutionA toroidal solenoid with air core has an average radius of 15cm, area of cross section and has 2000 turns. Calculate the self- inductance of the toroid. Assume the field to be uniform across the cross-section of the toroid.
View SolutionA solenoid is of length and has a radius of . It has turns. Around its central section a coil of turns is wound. Calculate the mutual inductance of the system.
View SolutionA solenoid is of length 50 cm and has a radius of 2cm. It has 500 turns. Around its central section a coil of 50 turns is wound. Calculate the mutual inductance of the system.
View SolutionA solenoid is of length 50cm and has a radius of 2cm. It has 500 turns. Around its central section of coil of 50 turns is wound. Calculate the mutual inductance of the system.
View SolutionA solenoid is of length 50 cm and has a radius of 2cm. It has 500 turns. Around its central section a coil of 50 turns is wound. Calculate the mutual inductance of the system.
View SolutionA solenoid is of length 50 cm and has a radius of 2cm. It has 500 turns. Around its central section a coil of 50 turns is wound. Calculate the mutual inductance of the system.
View SolutionA solenoid of 1000 turns is wound over a length of 40 cm. The area of cross section is . Around its central section, a coil of 500 turns is closely wound. If an initial current of 1 A in the solenoid is reversed in 0.3 s, find the emf induced in the coil.
View SolutionCalcualte the self-inducatance of the air cored solined of length 80 cm and has 500 turns and its cicular cross- section has diamter of 2 cm.
View SolutionAn charge is given to the capacitor in the circuit shown in Fig. so thae upper plate A is positively charged. An unknown resistance R is connected in the left limb. As soon as the switch S in the central limb is closed, a current of 2 A flows through the resistor in the central limb. The capa citive time constant for the circuit is

View SolutionAn 80 muC charge is given to the 4muF capacitor in the circuit shown in Fig. so thae upper plate A is positively charged. An unknown resistance R is connected in the left limb. As soon as the switch S in the central limb is closed, a current of 2 A flows through the 2Omega resistor in the central limb. The capa citive time constant for the circuit is
View SolutionThe cross-sectional area of the left limb of a U-tube is one-third of that of its right limb. It contains some mercury. The empty space in the left limb measures to 40 cm. If water is poured to fill it up, then find the rise of the mercury column in the right limb. (Specific gravity of mercury = 13.6)
View Solution