A solenoid is of length 50cm and has a radius of 2cm. It has 500 turns. Around its central section a coil of 50 turns is wound. Calculate the mutual inductance of the system.
To calculate the mutual inductance of the system consisting of a solenoid and a coil wound around it, we will follow these steps:
Step 1: Identify the parameters of the solenoid
- Length of the solenoid (L) = 50 cm = 0.5 m
- Radius of the solenoid (R) = 2 cm = 0.02 m
- Number of turns in the solenoid (N₁) = 500 turns
Step 2: Calculate the number of turns per unit length (n₁) of the solenoid
The number of turns per unit length (n₁) is given by:
n₁=N₁L
Substituting the values:
n₁=500 turns0.5 m=1000 turns/m
Step 3: Identify the parameters of the coil
- Number of turns in the coil (N₂) = 50 turns
Step 4: Calculate the magnetic field (B) inside the solenoid
The magnetic field inside a long solenoid is given by:
B=μ0n₁I1
Where:
- μ0 (permeability of free space) = 4π×10−7H/m
- I1 is the current flowing through the solenoid.
Step 5: Calculate the area (A) of the coil
The area of the coil is given by:
A=πR2
Substituting the radius:
A=π(0.02 m)2=π×0.0004 m2=0.00125664 m2
Step 6: Calculate the magnetic flux (Φ) through the coil
The magnetic flux through the coil is given by:
Φ=B⋅A=μ0n₁I1A
Substituting the values:
Φ=(4π×10−7)⋅(1000)⋅I1⋅(0.00125664)
Step 7: Calculate the mutual inductance (M)
The mutual inductance (M) is defined as:
Φ=M⋅I1
From the above equation, we can express M as:
M=μ0n₁N₂A
Substituting the values:
M=(4π×10−7)⋅(1000)⋅(50)⋅(0.00125664)
Step 8: Calculate the value of M
Calculating the value:
M=(4π×10−7)⋅(1000)⋅(50)⋅(0.00125664)
M≈0.00007898H
Converting to microhenries:
M≈78.98μH
Final Answer
The mutual inductance of the system is approximately 78.98μH.
---
- Length of the solenoid (L) = 50 cm = 0.5 m
- Radius of the solenoid (R) = 2 cm = 0.02 m
- Number of turns in the solenoid (N₁) = 500 turns
The number of turns per unit length (n₁) is given by:
n₁=N₁L
Substituting the values:
n₁=500 turns0.5 m=1000 turns/m
- Number of turns in the coil (N₂) = 50 turns
The magnetic field inside a long solenoid is given by:
B=μ0n₁I1
Where:
- μ0 (permeability of free space) = 4π×10−7H/m
- I1 is the current flowing through the solenoid.
The area of the coil is given by:
A=πR2
Substituting the radius:
A=π(0.02 m)2=π×0.0004 m2=0.00125664 m2
The magnetic flux through the coil is given by:
Φ=B⋅A=μ0n₁I1A
Substituting the values:
Φ=(4π×10−7)⋅(1000)⋅I1⋅(0.00125664)
The mutual inductance (M) is defined as:
Φ=M⋅I1
From the above equation, we can express M as:
M=μ0n₁N₂A
Substituting the values:
M=(4π×10−7)⋅(1000)⋅(50)⋅(0.00125664)
Calculating the value:
M=(4π×10−7)⋅(1000)⋅(50)⋅(0.00125664)
M≈0.00007898H
Converting to microhenries:
M≈78.98μH
The mutual inductance of the system is approximately 78.98μH.
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:C.U.Q 1
Explore 51 Videos
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Assertion & Reason
Explore 11 Videos
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -4
Explore 43 Videos
- ELECTRO MAGNETIC WAVESBook:NARAYNAChapter:ELECTRO MAGNETIC WAVESExercise:LEVEL-II(H.W)
Explore 14 Videos
Similar Questions
A long solcnoid of length 1m, cross-sectional area 10cm2, having 1000 turns has wound about its centre a small coil of 20 turns. Compute the mutual inductance of the pair of solenoid and the coil . What is the induced EMF in the coil when the current in the solenoid changes at the rate of 10A/s?
View SolutionA solenoid of 1000 turns is wound over a length of 40 cm. The area of cross section is 20cm2. Around its central section, a coil of 500 turns is closely wound. If an initial current of 1 A in the solenoid is reversed in 0.3 s, find the emf induced in the coil.
View Solution
Knowledge Check
A solenoid of length 50 cm and a radius of cros section 1 cm has 1000 turns of wire wound over it if the current carried is 5A the magnetic field on its axis near the centre of the solenoid is approximately (Given permeability of free space μ0=4π×10−7T−mA−1)
A0.63×10−2TB1.26×10−2TC2.51×10−2TD6.3TA solenoid having 500 turns and length 2 m has radius of 2 cm , the self inductance of solenoid
A4×10−4HB2×10−4HC8×10−4HD16×10−4HA long solenoid of length L, cross section A having N1 turns has about its center a small coil of N2 turns as shows in Fig The mutual inductance of two circuits is
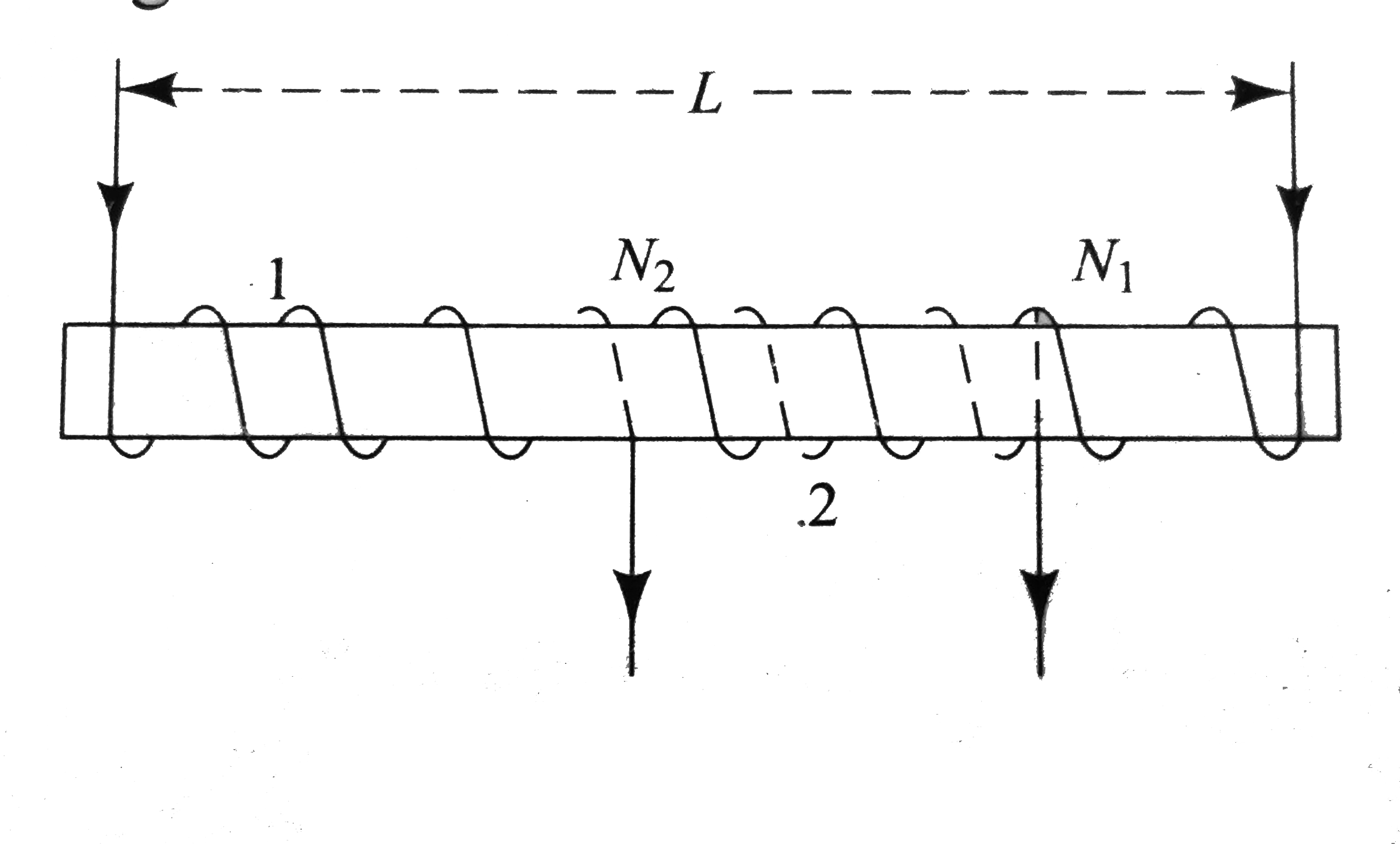 Aμ0A(N1/N2)LBμ0A(N1N2)LCμ0AN1N2LDμ0AN21N2L
Aμ0A(N1/N2)LBμ0A(N1N2)LCμ0AN1N2LDμ0AN21N2L
Over a solenoid of 50 cm length and 2 cm radius having 500 turns. Is wound another wire of 50 turns near the centre. Calculate mutual inductance of the two coils. If currents in primary changes From 0 to 5 a in 0.02 s, what is the emf induced in secondary coil ?
View SolutionA coil having 800 turns, area of cross section 12cm2 and 15 cm long is connected in series with another coil having 500 turns, area of cross section 10cm2 and 10 cm long. Calculate the net inductance of the system.
View SolutionA 2 m long solenoid with diameter 4 cm and 2000 turns has a secondary of 1000 turns wound closely near its mid point. Calculate the mutual inductance between the two coils.
View SolutionA straight solenoid has 50 turns per cm in primary and total 200 turns in the secondary. The area of cross section of the solenoids is 4cm2. Calculate the mutual inductance. Primary is tightly kept in side the secondary.
View SolutionA 2 m long solenoil with diameter 2 cm and 2000 turns has a secondary coil of 1000 turns wound closely near its midpoint. The mutuat inductance between the two coils is.
View Solution

