A belt is stretched over two identical pulleys of diameter D meter. The initial tension in the belt throughout is 2.4KN when the pulleys are at rest. In using these pulleys and belt to transmit torque it is found that the increase in tension on one side is equal to the decrease on the other side. Find the maximum torque that can be transmitted by the belt drive given that the coefficient of friction between belt and pulley is 0.30.
Given data: Diameter of both pulley = D Initial tension in belt TO =2.4KN Torque = ? Coefficient of friction µ = 0.3 Since dia of both pulley are same i.e. Angle of contact = π TO = T1 + T2/2 T1 + T2 = 4.8KN ............i Now Ratio of belt tension = T1/T2 = eµθ T1/T2 = e0.3π T1 = 2.566T2 ......ii Putting the value of ii in equation i We get T1 = 3.46KN T2 = 1.35KN Now Maximum torque transmitted by the pulley = T1 – T2D/2 Since radius of both pulley are same Torque = 3.46 – 1.35D/2 = 1.055D KN–m Torque = 1.055D KN-m.
Related Solutions
An air compressor is powered by a 200 rad/s electric motor using a V-belt drive. The motor pulley is 8 cm in radius, and the tension in the V-belt is 135 N on the side and 45N on the other. The power of the motor will be
View SolutionAn elastic belt is placed around the rim of a pulley of radius 5cm. From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at point P,10cm from the point O. Find the length of the belt that is still in contact with the pulley, also find the area of the shaded region.
View Solution5 सेमी त्रिज्या की के पुली रिम पर प्रत्यास्थ (elastic) बेल्ट रखी है बेल्ट के एक बिंदु को केंद्र O से 10 सेमी दूर बिंदु P तक खींचा जाता है पुली के रिम के संपर्क में आने बेल्ट की लम्बाई ज्ञात कीजिए ।
View SolutionA flexible drive belt runs over a frictionless flywheel (see Figure). The mass per unit length of the drive belt is 1 kg/m, and the tension in the drive belt is 10N. The speed of the drive belt is 2m/s. The whole system is located on a horizontal plane. Find the normal force (in N) exerted by the belt on the flywheel.
View SolutionA flexible drive belt runs over a frictionless flywheel (see Figure). The mass per unit length of the drive belt is 1 kg/m, and the tension in the drive belt is 10N. The speed of the drive belt is 2m/s. The whole system is located on a horizontal plane. Find the normal force (in N) exerted by the belt on the flywheel.
View SolutionA flexible drive belt runs over a frictionless flywheel (see Figure). The mass per unit length of the drive belt is 1 kg/m, and the tension in the drive belt is 10N. The speed of the drive belt is 2m/s. The whole system is located on a horizontal plane. Find the normal force (in N) exerted by the belt on the flywheel.
View Solutionएक 5 सेमी त्रिज्या वाली पुली के चारों ओर लचीली बेल्ट चढ़ायी जाती है | बेल्ट के एक बिन्दु को पुली के केन्द्र O से सीधा P बिन्दु तक 10 सेमी तक खिंचा जाता है | पुली की रिम पर बचे हुए बेल्ट की लम्बाई ज्ञात कीजिए तथा छायांकित भाग का क्षेत्रफल भी ज्ञात कीजिए |
View SolutionAn elastic belt is placed round the rim of a pulled of radius 5cm. One point on the belt is pulled directly away from the centre of the pulley until it is at P, 10cm from O. Find the length of the belt that is in contact with the rim of the pulley. Also, find the shaded area.
View SolutionAn elastic belt is placed around the rim of a pulley of radius 5 cm (Fig.) From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also, find the shaded area.[use pi=3.14 and sqrt3=1.73]
View SolutionThe flexible belt on a flywheel is moving (see diagram). The drive belt has a mass per length of 1 kg / m and the tension in the belt is 10 N. The speed of the belt is 2m / s. The entire body is located on the horizontal plane. Find the force (in N) exerted by the belt on the flywheel.
View Solutionपुली के ऊपर चलने वाले संवाहक पट्टों (conveyor belts) के ऊपर धातु का पतला कोट किया जाता है। क्यों?
View SolutionA belt moves over two pulleys A and B as shown in the figure. The pulleys are mounted on two fixed horizontal axles. Radii of the pulleys A and B are 50 cm and 80 cm respectively. Pulley A is driven at constant angular acceleration of 0.8 unitl pulley B acquries an angular velocity of 10 rad/s. The belt does not slide on either of the pulleys.
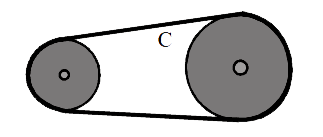
(a)Find the acceleration of a point C on the belt and angular acceleration of the pulley B.
(b) How long does it take for the pulley B to acquire an angular velocity of 10 rad/s ?
View SolutionA belt is moving over two pulleys A and B as shown in the figure. The pulleys are connected on two fixed horizontal axles. The radii of pulleys A and B are 50 cm and 80 cm respectively. pulley A has a constant angular acceleration 0 . 8 rad // s^(2) A is then driven until pulley B attains an angular velocity of 10 rad/s. Belt does not slip on any pulley (a) Find the acceleration of point C on the belt and the angular acceleration of pulley B. (b) How long will pulley B take to attain an angular velocity of 10 rad/s?
View Solutionचित्रानुसार एक बेल्ट दो घिरनियों A व B के ऊपर गति कर रही है। घिरनियों को दो स्थिर क्षैतिज धुरियों पर जोड़ा गया है । घिरनियों A व B की त्रिज्याएँ क्रमशः 50 cm व 80 cm है। घिरनी A को एक नियत कोणीय त्वरण से तब एक चलाया जाता है जब तक कि घिरनी B, 10 rad / s का कोणीय वेग प्राप्त न कर ले। बेल्ट किसी भी घिरनी पर फिसलती नहीं है

(a) बेल्ट पर C बिन्दु का त्वरण तथा घिरनी B का कोणीय त्वरण ज्ञात कीजिए ।
(b) घिरनी B, 10 rad / s का कोणीय वेग प्राप्त करने में कितना समय लेगी ?
View Solutionएक कम्पनी दो प्रकार A और B के लेकर बैल्ट बनाता है | दोनों प्रकार के बैल्ट पर क्रमशः ₹ 2 तथा ₹ का लाभ होता है | बैल्ट A के निर्माण में बैल्ट B की तुलना में दो गुना समय लगता है | यदि सभी बैल्ट B प्रकार के हो तो कम्पनी प्रतिदिन 1,000 बैल्ट उत्पादित कर सकती है लेकिन प्रतिदिन 800 बैल्ट के लिए ही लेदर उपलब्ध है (A और B के लिए )बैल्ट A को फैंसी बक्क्ल की आवश्यकता है और यह प्रतिदिन केवल 400 बैल्ट के लिए ही उपलब्ध है | बैल्ट B के लिए प्रतिदिन 700 बक्क्ल उपलब्ध है |
View Solutionएक कंपनी A और B दो प्रकार की चमड़े की बेल्ट बनाती है । दोनों बेल्टों पर लाभ क्रमशः Rs 40 और Rs 30 प्रति बेल्ट है । A प्रकार की एक बेल्ट बनाने में, B प्रकार की एक बेल्ट बनाने से दो गुना समय लगता है । यदि सभी बेल्ट B प्रकार की है, तो कंपनी 1000 बेल्ट प्रतिदिन बना सकती है, परन्तु चमड़े की पूर्ति केवल 800 बेल्ट प्रतिदिन के लिये पर्याप्त है । बेल्ट A के फेन्सी बक्कल केवल 400 बक्कल प्रतिदिन उपलब्ध है । बेल्ट B के साधारण बक्कल केवल 700 बक्कल प्रतिदिन उपलब्ध है । अधिकतम लाभ के लिये कंपनी को दोनों प्रकार की कितनी बेल्ट बनानी चाहिये, आलेख विधि से हल कीजिए ।
View SolutionAn elastic belt is placed round the rim of a pulled of radius 5cm. One point on the belt is pulled directly away from the centre of the pulley until it is at P, 10cm from O. Find the length of the belt that is in contact with the rim of the pulley. Also, find the shaded area.
View SolutionSeat belts in cars are called safety belts. Why?
View Solution............... founded the Green Belt Movement
View Solutionएक कम्पनी A और B नमूने की दो चमड़े की बेल्ट बनाती हैं । बेल्ट A उच्च कोटि की एंव बेल्ट B घटिया कोटि की हैं । दोनों बेल्टों पर लाभ क्रमशः 40 तथा 30 रुपये प्रति बेल्ट हैं । A प्रकार की एक बेल्ट के बनाने में B किस्म की एक बेल्ट बनाने से दोगुना समय लगता हैं । यदि सब बेल्ट B नमूने की हों तो कम्पनी 1000 बेल्ट प्रतिदिन बना सकती हैं । लेकिन चमड़े की पूर्ति केवल 800 ( A और B दोनों को मिलाकर ) बेल्ट प्रतिदिन के लिए पर्याप्त हैं । बेल्ट A के लिए एक फेन्सी बक्कल चाहिए और उसके लिए केवल 400 बक्कल प्रतिदिन प्राप्त हैं । बेल्ट B के लिए केवल 700 बक्कल प्रतिदिन प्राप्त है । अधिकतम लाभ के लिए कम्पनी दोनों तरह की बेल्ट कितनी बनाए , आलेख विधि से हल करते हुए ज्ञात कीजिए ?
View Solution