A horizontal drum of a belt drive carries the belt over a semicircle around it. It is rotated anticlockwise to transmit a torque of 300N-m. If the coefficient of friction between the belt and rope is 0.3 calculate the tension in the limbs 1 and 2 of the belt shown in figure and the reaction on the bearing. The drum has a mass of 20Kg and the belt is assumed to be mass less.
Given data: Torquet = 300N-m Coff. of frictionµ = 0.3 Diameter of Drum D = 1m R = 0.5m Mass of drumm = 20Kg. Since angle of contact = π rad Torque = T1 – T2.R 300 = T1 – T2 X 0.5 T1– T2 = 600N ...i And T1/T2 = eµθ T1/T2 = e0.3π T1 = 2.566T2 ...ii Solving i and iiWe get T1 = 983.14NT2 = 383.14NNow reaction on bearing is opposite to the mass of the body and it is equal to R = T1 + T2 + mg R = 983.14 + 383.14 + 20 X 9.81 R = 1562.484N.
Related Solutions
A flexible drive belt runs over a frictionless flywheel (see Figure). The mass per unit length of the drive belt is 1 kg/m, and the tension in the drive belt is 10N. The speed of the drive belt is 2m/s. The whole system is located on a horizontal plane. Find the normal force (in N) exerted by the belt on the flywheel.
View SolutionA flexible drive belt runs over a frictionless flywheel (see Figure). The mass per unit length of the drive belt is 1 kg/m, and the tension in the drive belt is 10N. The speed of the drive belt is 2m/s. The whole system is located on a horizontal plane. Find the normal force (in N) exerted by the belt on the flywheel.
View SolutionA flexible drive belt runs over a frictionless flywheel (see Figure). The mass per unit length of the drive belt is 1 kg/m, and the tension in the drive belt is 10N. The speed of the drive belt is 2m/s. The whole system is located on a horizontal plane. Find the normal force (in N) exerted by the belt on the flywheel.
View SolutionThe flexible belt on a flywheel is moving (see diagram). The drive belt has a mass per length of 1 kg / m and the tension in the belt is 10 N. The speed of the belt is 2m / s. The entire body is located on the horizontal plane. Find the force (in N) exerted by the belt on the flywheel.
View SolutionA block is gently placed on a conveyor belt moving horizontally with constant speed.After 4s the velocity of the block becomes equal to the velocity of belt If the coefficient of friction between the block and the belt is 0.2,then velocity of the conveyor belt is
View SolutionA block is placed on the belt moving in the horizontal with uniform speed. After 4 seconds the velocity of the block becomes equal to the velocity of the belt. If the coefficient of friction between the block and the belt is 0.2 then the velocity of the moving belt is
View SolutionA block is gently placed on a conveyor belt moving horizontally with constant speed. After t = 4s, the velocity of the block becomes equal to the velocity of the belt. If the coefficient of friction between the block and the belt is mu = 0.2, then the velocity of the conveyor belt is
View SolutionA block is gently placed on a conveyor belt moving horizontally with constant speed. After t = 4s, the velocity of the block becomes equal to the velocity of the belt. If the coefficient of friction between the block and the belt is mu = 0.2, then the velocity of the conveyor belt is
View SolutionA block is gently placed on a conveyor belt moving horizontal with constant speed After t = 4s the velocity of the block becomes equal to velocity of the belt If the coefficient of friction between the block and the belt is mu = 0.2 , then the velocity of the conveyor belt is .
View SolutionA block is gently placed on a conveyor belt moving horizontal with constant speed After the velocity of the block becomes equal to velocity of the belt If the coefficient of friction between the block and the belt is , then the velocity of the conveyor belt is .
View SolutionFigure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with 1 m s^(-2) . What is the net force on the man? If the coefficient of static friction between the man’s shoes and the belt is 0.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt ? (Mass of the man = 65 kg.)
View SolutionFigure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with . What is the net force on the man? If the coefficient of static friction between the man’s shoes and the belt is 0.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt ? (Mass of the man = 65 kg.)
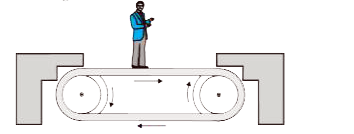
View SolutionFigure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with . What is the net force on the man? If the coefficient of static friction between the man’s shoes and the belt is 0.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt ? (Mass of the man = 65 kg.)
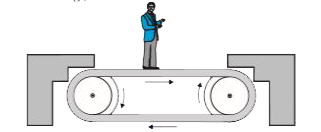
View SolutionA man standing stationary with respect to a horizontal conveyor belt that is accelerating with 1 m s- 2 . What is the net force on the m an ? If the coefficient of static friction between the man’s shoes and the belt is 0.2 up to what acceleration o f the belt can the man continue to be stationary relative to the belt ? (Mass of the man = 65 kg).
View SolutionFigure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with l 1 ms^(-2) . The net force on the man, if the coefficient of static friction between the man's shoes and the belt is 0.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt (mass of the man-65kg)
View SolutionFigure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with 1 ms^(-2) . What is the net force on the man ? If the coefficient of static friction between the man's shoes and the belt is 0.02 , up to what acceleration of the belt can the man continue to be stationary relative to the belt ? (Mass of the man = 65 kg )
View SolutionA belt passes over a wheel of radius 25 cm. If a point on the belt has a speed of 5 m//s , the belt is moving with an angular velocity of
View SolutionAn object is gently placed on a long conveyer belt moving with a speed of 5 ms^(-1) If the coefficient of friction between the object and the belt is 0.5, the block will slide on the belt up to a distance (Take g = 10 m s^(-2) )
View SolutionA horizontal conveyor belt is moving at a speed of 5m/s. A box of mass 20kg is gently placed on this belt. Box first slips on the belt and finally comes to rest with respect to belt. If box takes time 0.1 s to stop slipping on the belt, then what will be the distance travelled by the box during this interval?
View SolutionA package rest on a conveyor belt which is initially at rest . The belt is started and moves to the right for with a constant acceleration of . The belt then moves with a constant deceleration and comes to a stop after a total displacement of . Knowing that the coefficient of friction between the package and the belt are and , determine (a) the deceleration of the belt , (b) the displacement of the package relative to the belt as the belt comes to a stop.

View Solution