A single story frame consists of two rigid columns with negligible masses a rigid beam of mass m and a spring-dashpot system as shown in Fig. The ground is forced to vibration by an earthquake; the acceleration ¨uE = b0cos Ωt is known from measurements. Determine the maximum amplitude of the steady state vibrations. Assume that the system is underdamped and that the vibrations have
We assume that the amplitudes of the vibrations are small. Then the elongation of the diagonal is obtained as The elongation produces the force in the spring-dashpot system see the figure. The equation of motion of the beam is given by Thus the relative displacement y=x-υEis described by The maximum amplitude A is obtained for η = Ω/ω ≈ 1 resonance!. In the case of small damping ζ ≪ 1 we obtain
Related Solutions
A body of mass is released from a height h to a scale pan hung from a spring. The spring constant of the spring is , the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k , the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionA body of mass is released from a height h to a scale pan hung from a spring. The spring constant of the spring is , the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View Solutionअगर m द्रव्यमान को एक स्प्रिंग से लटकाया जाता है, तो स्प्रिंग 6 cm बढ़ जाती है। यदि भारित स्प्रिंग को नीचे की तरफ थोड़ा खींचकर छोड़ दिया जाता है, तो उस निकाय का कम्पन-काल क्या होगा?
View SolutionInstrument used to measure the vibrations of earthquake ?
View SolutionA load of mass m falls from a height h on the scale pan hung from a spring as shown. If the spring constant is k and the mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is
View SolutionStatements: - Spring mass system without damping is a free vibration system. Reason: It has 3 degrees of freedom.
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
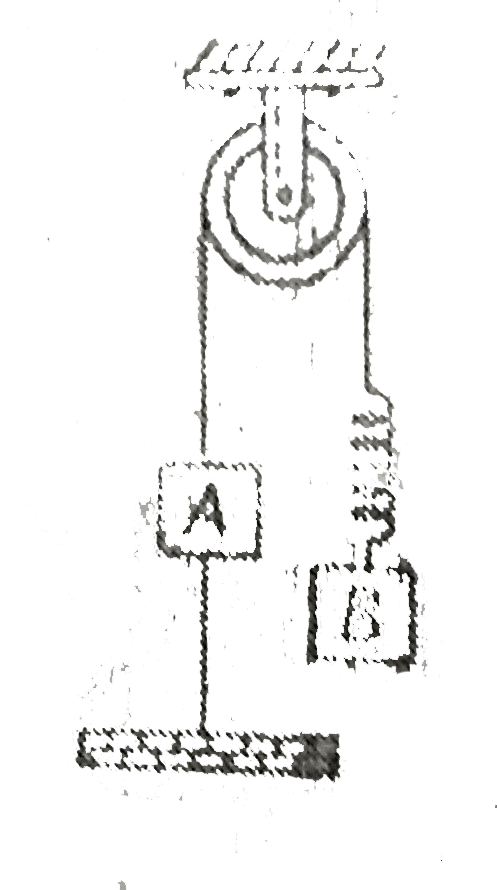
View SolutionTwo bodies M and N of equal mass are hung separtely from two lightweight springs. Force constants of the springs are k_1 and k_2 . The bodies are set to vibrate so that their maximum velocities are equal. Find the ratio of the amplitudes of vibration of the two bodies.
View SolutionThe state (or) condition of vibration of a vibrating body is known is
View SolutionA vibrating system consists of mass 12.5 kg, a spring of spring constant 1000 (N ) /( m ) performing damped oscillation with damping coefficient of 15 kg s^(-1) . The value of critical damping coefficient of the system is
View SolutionA vibrating system consists of mass 12.5 kg, a spring of spring constant 1000 (N ) /( m ) performing damped oscillation with damping coefficient of 15 kg s^(-1) . The value of critical damping coefficient of the system is
View SolutionA vibrating system consists of mass 12.5 kg, a spring of spring constant 1000 (N ) /( m ) performing damped oscillation with damping coefficient of 15 kg s^(-1) . The value of critical damping coefficient of the system is
View SolutionOn suspending a mass m from a spring of force constant k, frequency of vibration f is obtained. If a second spring as shown in the figure, is arranged then the frequency will be :
View SolutionA simple pendulum of length L having bob of mass M is vibrating with amplitude a. Then the maximum tension in the string is
View SolutionA simple pendulum of length l having bob of mass M is vibrating with amplitude a. Then the maximum tension in the string is
View SolutionA simple pendulum of length l having bob of mass M is vibrating with amplitude a. Then the maximum tension in the string is
View SolutionTwo vibrating systems are in resonance when
View SolutionTwo vibrating systems are in resonance when
View Solution