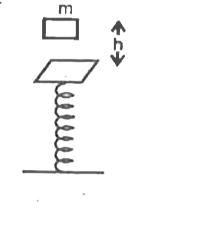
A body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

A

$\frac{m g}{k}$

B

$\frac{m g}{k} \sqrt{1 + \frac{2 h k}{m g}}$

C

$\frac{m g}{k} + \frac{m g}{k} \sqrt{\frac{1 + 2 h k}{m g}}$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:b

From the conservation principle,
$m g h = \frac{1}{2} k X_{0}^{2} - m g X_{0}$
where , $X_{0}$ is maximum elongation in spring.
$\Rightarrow \frac{1}{2} k X_{0}^{2} - m g X_{0} - m g h = 0$
$\Rightarrow X_{0}^{2} - \frac{2 m g}{k} X_{0} - \frac{2 m g}{k} h = 0$
$X_{0} = \frac{2 \frac{m g}{k} \pm \sqrt{{(\frac{2 m g}{k})}^{2} + 4 \times \frac{2 m g}{k}} h}{2}$
Amplitude = elongation in spring for lowest extreme position - elongation in spring for equilibrium position
$= X_{0} - X_{1} = \frac{m g}{k} \sqrt{(1 + \frac{2 h k}{m g}) [∵ X_{1} = \frac{m g}{k}]}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A body of mass m falls from a height h on a pan ( of negligible mass ) of spring balance as shwon. The spring is ideal and has a spring contant k. Just after striking the pan, the body sticks with the pan and starts oscillatory motion in vertical direction. The velocity of the body at mean position will be

A $\sqrt{2 m g^{2} k + 2 g h}$
B $\sqrt{\frac{k 2 g h}{m}}$
C $\sqrt{\frac{m g^{2}}{k} + 2 g h}$
D $\sqrt{\frac{m g^{2}}{k} + 4 g h}$
Question 2 - Select One
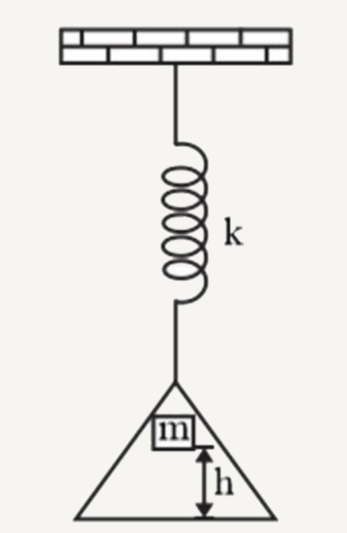
A load of mass m falls from a height h on to the scale pan hung from a spring as shown in the adjoining figure. If the spring constant is k and mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is

A $\frac{m g}{k}$
B $\frac{m g}{k} \sqrt{(\frac{1 + 2 h k}{m g})}$
C $\frac{m g}{k} + \frac{m g}{k} \sqrt{(\frac{1 + 2 h k}{m g})}$
D $\frac{m g}{k} \sqrt{(\frac{1 + 2 h k}{m g} - \frac{m g}{k})}$
Question 3 - Select One
A body of mass $m$ is released from a height h to a scale pan hung from a spring. The spring constant of the spring is $k$ , the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
A $\frac{m g}{k} \sqrt{1 - \frac{2 h k}{m g}}$
B $\frac{m g}{k}$
C $\frac{m g}{k} + \frac{m g}{k} \sqrt{1 + \frac{2 h k}{m g}}$
D $\frac{m g}{k} - \frac{m g}{k} \sqrt{1 - \frac{2 h k}{m g}}$

BITSAT GUIDE-SOLVED PAPER 2017 -(PART -I) PHYSICS

Home
Ask Doubt
Profile