A homogeneous circular disk of weight W = mg is suspended from a pin-supported bar of negligible mass. Initially the disk rotates with the angular velocity ω0. a Determine the amplitude of oscillation of the pendulum if the bar suddenly prevents the disk from rotating. b Calculate the energy loss ∆E
a First we determine the angular velocity ω of the bar immediately after the rotation of the disk is prevented note that the bar is still in the vertical position. Since there are no external moments acting with respect to A the angular momentum is conserved. With The maximum value ϕ1 of the angle ϕ = amplitude of the oscillation can be calculated from the conservation of energy:T1+V1 =T0+V0If we choose the potential energy V0 initial position to be equal to zero we can writeThen conservation of energy leads tob The loss of energy ∆E is given by the difference ∆T of the kinetic energies before and after the blocking:
Related Solutions
जड़त्व आघूर्ण की एक वृत्ताकार डिस्क अपनी सममिति अक्ष के परितः, एक स्थिर कोणीय वेग से क्षैतिज तल में घूर्णन कर रही है। इस डिस्क के ऊपर जड़त्व आघूर्ण की एक अन्य डिस्क संकेन्द्री डाल दी जाती है। प्रारंभ में दूसरी डिस्क की कोणीय चाल शून्य है। अन्ततः दोनों डिस्क एक ही स्थिर कोणीय वेग से घूर्णन करने लगती हैं। प्रारंभ में घूर्णन करती हुई डिस्क की घर्षण के कारण नष्ट हुई ऊर्जा है ।
View Solutionநிலைமத் திருப்புத் திறன் கொண்ட வட்டத்தட்டு மாறாத கோண திசைவேகம் வுடன் கிடைத்தளத்தில் சமச்சீரான அச்சைப் பற்றி சுழல்கிறது. ஓய்வு நிலையிலுள்ள மற்றொரு வட்டத்தட்டின் என்ற நிலைமத்திருப்புத்திறனுடன் சுழலும் வட்டத்தட்டின் மீது அச்சுழலும் அச்சிலேயே விடப்படுகிறது. இதனால் இரு வட்டத்தட்டுகளும் மாறா கோண வேகத்தில் சுழல்கிறது. இந்நிகழ்வில் உராய்வினால் ஏற்படும் ஆற்றல் இழப்பு
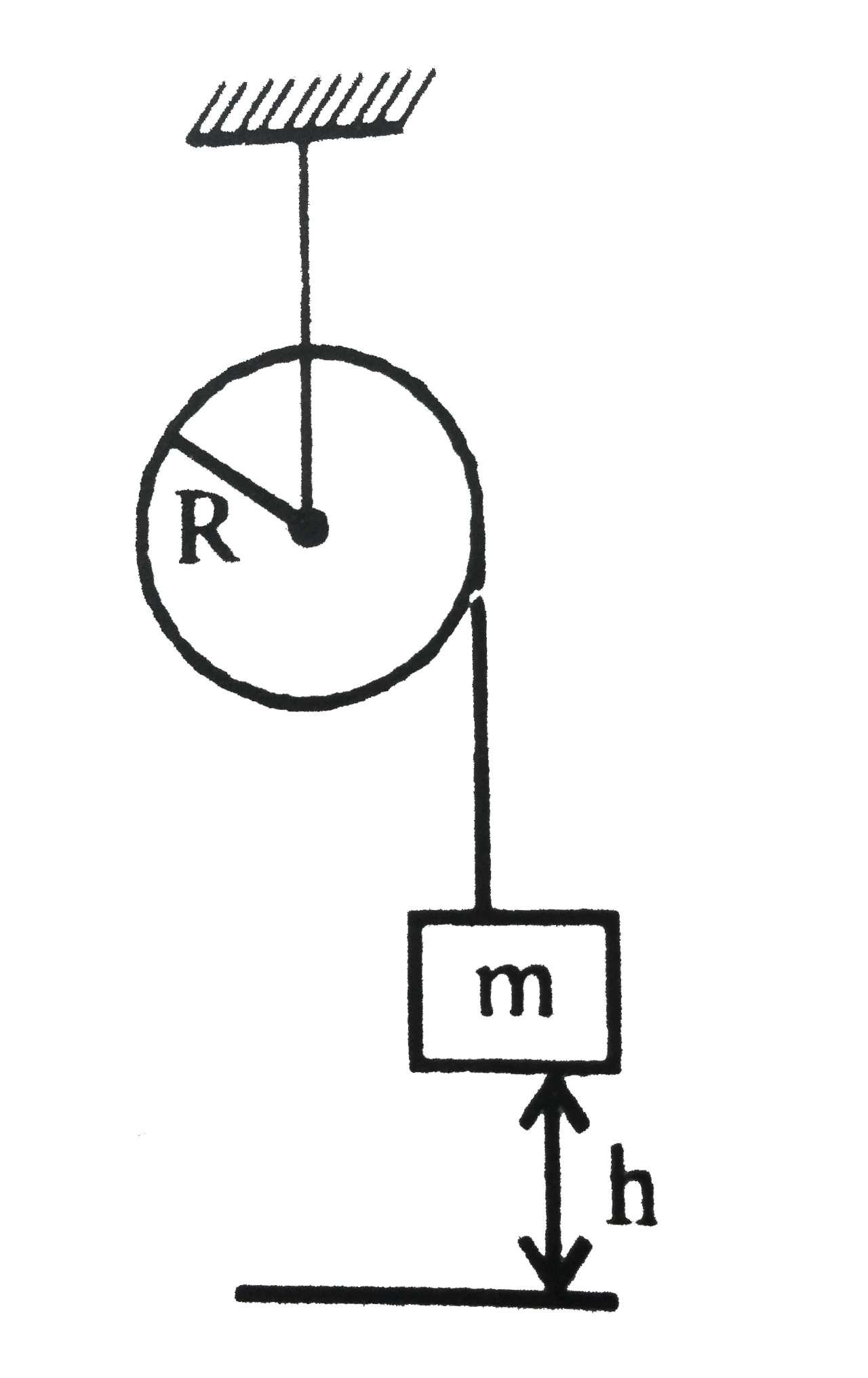
View SolutionA mass is attached to a pulley through a cord as shown in figure. The pulley is a solid disk with radius . The cord does not slip on the disk. The mass is released from rest at a height from the ground and at the instant the mass reaches the ground, the disk is rotating with angular velocity . Find the mass of the disk.
 .
.
View Solutionएक पतली वृत्ताकार चकती जिसका द्रव्यमान M तथा त्रिज्या r है, अपने अक्ष के अनुदिश नियत कोणीय वेग से घूर्णन कर रही है। दो वस्तुएँ जिनमें प्रत्येक का द्रव्यमान m है, चकती के व्यास के दोनों सिरों से मृदुलता से जुड़ी हैं। अब चकती जिस कोणीय वेग से घूर्णन करेगी वह है
View SolutionA circular disk of moment of inertia is rotating in a horizontal plane , about its symmetry axis , with a constant angular speed . Another disk of moment of inertia is dropped coaxially onto the rotating disk . Initially the second disk has zero angular speed . eventually both the disks rotate with a constant angular speed . The energy lost by the initially rotating disc to friction is
View SolutionTwo disks are rotating about the same axis. Disk A has a moment of inertia of and an angular velocity of . Disk B is rotating with an angular velocity of . The two disks are then linked together without the aid of any external torques, so that they rotate as a single unit with an angular velocity of . The axis of rotation for this unit is the same as that for the separate disks. What is the moment of inertia of disk B?
View SolutionA uniform disk of mass is rotating freely about a vertical axis through its centre with constant angular velocity A boy of mass starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionA uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity omega . A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionTwo solid semi-circular disks fo equal masses m=10 kg collide and stick together. Their initial velocities are shown initially not rotating. The combined object is a circular disk of radius 0.1 m it is spinning with an angular velocity omega=10rad//s . how much mechanical energy (in J ) is lost in collision ?
View SolutionA circular disk of moment of inertia I_t is rotating in a horizontal plane, about its symmetry axis,with a constant angular, speed omega_1 Another disk of moment of inertia I_b is dropped coaxially onto the rotating disk initially the second disk has zero angular speed.Eventually both the disks rotate with a constant angular speed omega_f The energy lost by the initially rotating disc to friction is :
View SolutionA thin circular disk of radius R is uniformly charged with density per unit area. The disk rotates about its axis with a uniform angular speed . The magnetic moment of the disk Is
View SolutionA thin circular disk of radius is uniformly charged with density per unit area.The disk rotates about its axis with a uniform angular speed .The magnetic moment of the disk is :
View SolutionA thin circular disk of radius is uniformly charged with density per unit area.The disk rotates about its axis with a uniform angular speed .The magnetic moment of the disk is :
View SolutionA cockroach of mass m lies on the rim of a uniform disk of mass 4.00 m that can rotate freely about its center like a merry-goround. Initially the cockroach and disk rotate together with an angular velocity of 0.320 rad/s. Then the cockroach walks halfway to the center of the disk. (a) What then is the angular velocity of the cockroach-disk system? (b) What is the ratio of the new kinetic energy of the system to its initial kinetic energy? ( c) What accounts for the change in the kinetic energy?
View Solutionसमान द्रव्यमान के एक वलय व डिस्क समान रेखीय वेग से बिना फिसले लुड़कते है यदि वलय की गतिज ऊर्जा 8 जूल है तो डिस्क की गति ऊर्जा होगी।
View Solutionजब कोई डिस्क एक समान कोणीय वेग से घूर्णन करती है, तो निम्नलिखित में कौन-सा कथन सत्य नहीं होता?
View Solutionजब कोई डिस्क एकसमान कोणीय वेग से घूर्णन करती है, तो निम्नलिखित में कौन-सा कथन सत्य नहीं होता?
View SolutionDisk 1 rotates about a smooth vertical axis with the angular velocity omega_(1) . Disk 2 rotating with the angular velocity omega_(2) is kept on disk 1 while rotating in the same direction. Find the change in the rotational kinetic energy of the system given that the moments of inertia of the disks relative to the rotation axis are equal to I_(1)andI_(2) , respectively. The constant surface of the disks are rough.
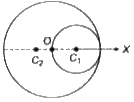
View Solutionत्रिज्या R की एक समान वृत्ताकार डिस्क से त्रिज्या R/4 की एक समाक्ष छोटी वृत्ताकार डिस्क काट ली गई है। यदि सम्पूर्ण डिस्क का केंद्र O हो तो शेष डिस्क के द्रव्यमान केंद्र की O से दूरी होगी
View SolutionConsider a disk of mass m , radius R lying on a liquid layer of thickness T and coefficient of viscosity eta as shown in the fig. The torque required to rotate the disk at a constant angular velocity Omega given the viscosity is uniformly eta .
View Solution