A point mass m is subjected to a central force F = mk2r where k is a constant and r is the distance of the mass from the origin 0. At time t = 0 the mass is located at P0 and has velocity components vx = v0 and vy = 0. Find the trajectory of the mass.
The equations of motion in the directions x and y are→: mx¨ = −F cosα ↑ : my¨ = −F sin α .With F = mk2r x = r cosα and y = r sin α we obtainx¨+k2x = 0 y¨+k2y = 0Both equations are equivalent to the differential equation that describes undamped free vibrations of a point mass The solutions arex = A cos kt + B sin kt y = C cos kt + D sin ktThe constants of integration are calculated from the initial conditions:We now have a parametric representation of the curve describing the motion:x = v0/k sin kt y = r0cos kt .To eliminate the time these equations are squared and then added. Thus we finally obtainThe point mass moves along an ellipse which reduces to a circle for k = v0/r0.
Related Solutions
A point mass m is located at (0,a). Where should the 2m mass be kept, so that centre of mass lies at origin
View Solutiona point mass (m) is located at (0,a) where should th 2m mass be kept ,so that centre of mass lies at origin?
View SolutionA particle of mass 'm' is at rest the origin at time t =0. It is subjected to a force F(t) = in the X-direction
View SolutionA particle of mass M originally at rest is subjected to a force whose direction is constant but magnitude varies with time according to the relation F=F_(0)[1-((t-T)/(T))^(2)] Where F_(0) and T are constants. The force acts only for the time interval 2T. The velocity v of the particle after time 2T is :
View SolutionThree identical points of mass 1 kg are located at the point ( 0 0 ) ( 0 , 2m 0 ) in the xy rhythm. The force of gravity on the mass at the origin will be
View SolutionA particle of rest mass starts moving at a moment due to a constant force F. Find the time dependence of the particle's velocity and of the distance covered.
View SolutionA particle whose initial mass is is projected vertically at time t= 0 with speed gT, where T is a constant. At time t the mass of the particle has increased to . If the added mass is at rest relative to particle when it is acquired
The mass of the particle at its highest point is
View SolutionA point mass m_(0) is placed at distance R//3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m_(0) is
View SolutionA force F = Be^(Ct) acts on a particle whose mass is m and whose velocity is 0 at t = 0. It's terminal velocity is :
View Solution1 kg किग्रा द्रव्यमान के तीन समरूप बिन्दु द्रव्यमान x-y तल में बिन्दु (0, 0) (0, 0.2 m) तथा (0.2 m, 0) पर स्थित है। मूल बिन्दु पर द्रव्यमान पर स्थित गुरूत्वीय बल होगा :
View SolutionA particle of mass m, moving in a circular path of radius R with a constant speed is located at point (2R, 0) at time t = 0 and a man starts moving with a velocity along the positive y-axis from origin at time t = 0. Calculate the linear momentum of the particle w.r.t. man as a function of time ______________.

View SolutionA particle of mass m, moving in a cicular path of radius R with a constant speed is located at point (2R,0) at time and a man starts moving with a velocity along the +ve y-axis from origin at time . Calculate the linear momentum of the particle w.r.t. the man as a function of time.
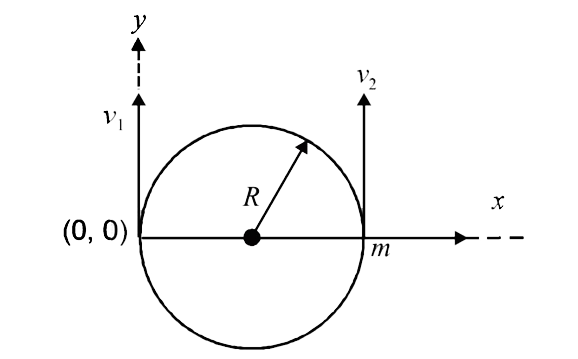
View SolutionA particle of mass m, moving in a cicular path of radius R with a constant speed v_2 is located at point (2R,0) at time t=0 and a man starts moving with a velocity v_1 along the +ve y-axis from origin at time t=0 . Calculate the linear momentum of the particle w.r.t. the man as a function of time.
View SolutionA particle of mass m is at rest at the origin at time It is subjected to a force in the X-direction. Its speed is depicted by which of the following curves
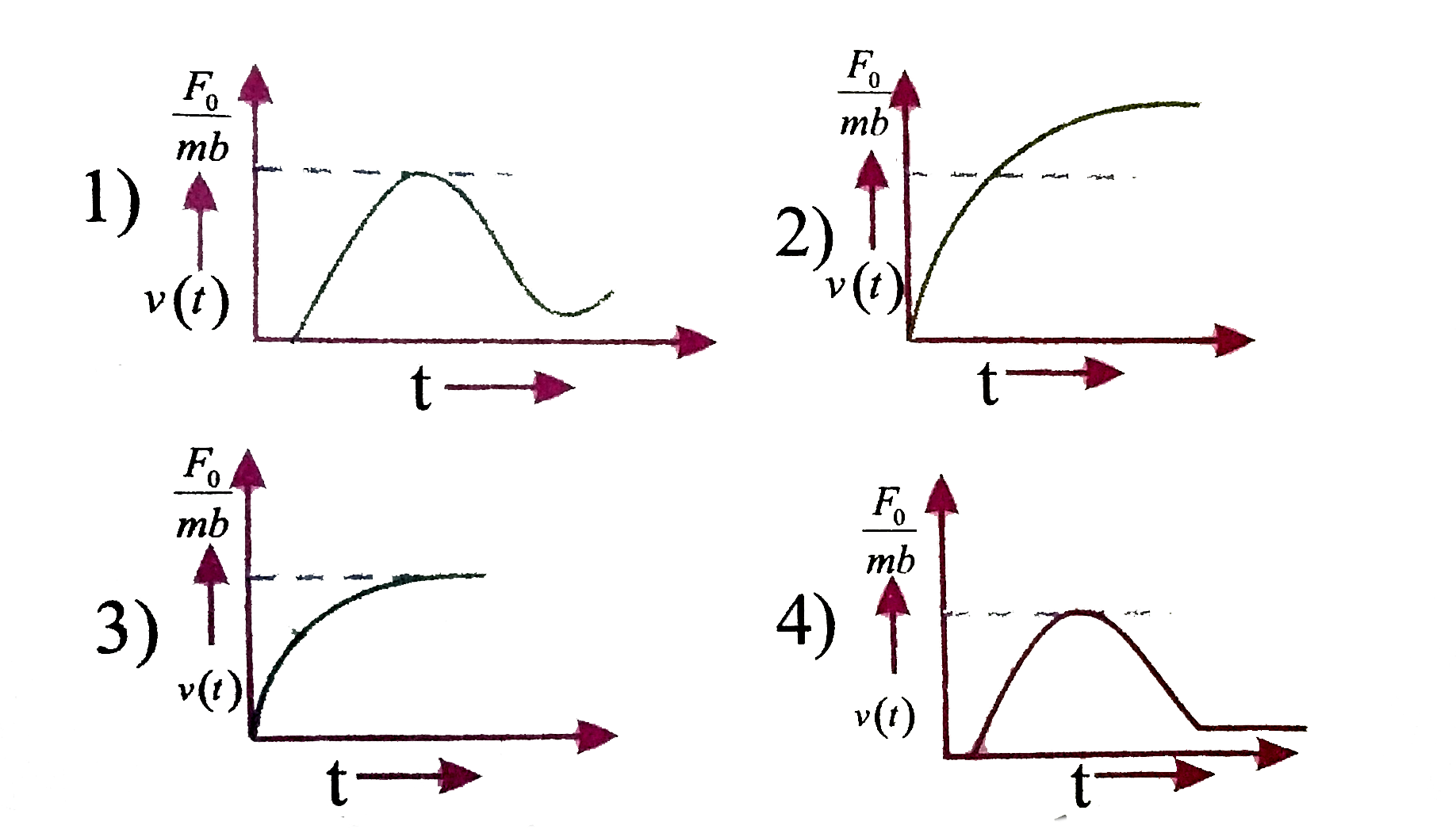
View SolutionA particle of mass m is at rest at the origin at time It is subjected to a force in the X-direction. Its speed is depicted by which of the following curves

View SolutionA particle of mass m is at rest at the origin at time t=0 . It is subjected to a force F(t)=F_(0)e^(-bt) in the X - direction. Its speed V(t) is depicted by which of the following curves.
View SolutionA particle of mass m is at rest at the origin at time t = 0.It is subjected to a force in the x direction. Its speed v(t) is depicted by which of the following curves ?
View SolutionA particle of mass m is at rest at the origin at time t=0. It is subjected to a force in the x direction. Its speed v(t) is depicted by which of the following curves ?
View SolutionA particle of mass m is at rest the origin at time t= 0 . It is subjected to a force F(t) = F_(0) e^(-bt) in the x - direction. Its speed v(t) is depicted by which of the following curves ?
View SolutionA particle of mass is at rest the origin at time . It is subjected to a force in the - direction. Its speed is depicted by which of the following curves ?
View Solution