A particle of mass m is at rest the origin at time t=0 . It is subjected to a force F(t)=F0e−bt in the x - direction. Its speed v(t) is depicted by which of the following curves ?
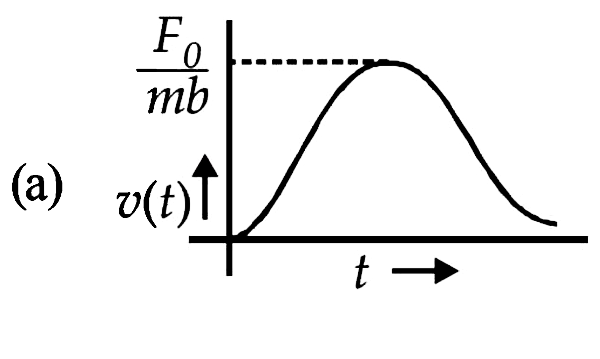
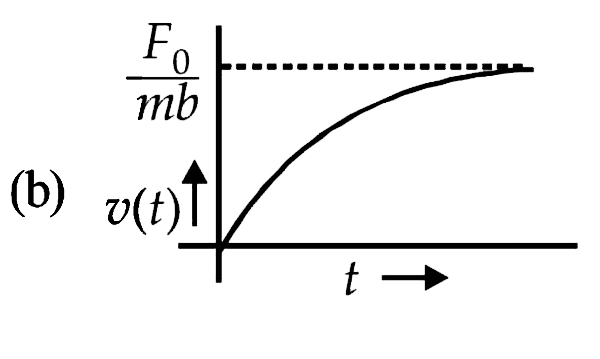

The correct Answer is:B
To solve the problem, we need to determine the velocity v(t) of a particle subjected to a force F(t)=F0e−bt in the x-direction. Here are the steps to derive the expression for velocity:
Step 1: Write down the relationship between force, mass, and acceleration.
We know from Newton's second law that:
F=m⋅a
where a is the acceleration. Since acceleration can also be expressed as the derivative of velocity with respect to time, we have:
F=m⋅dvdt
Step 2: Substitute the expression for force into the equation.
Given the force F(t)=F0e−bt, we can substitute this into the equation:
m⋅dvdt=F0e−bt
Step 3: Rearrange the equation to isolate dv.
Rearranging gives us:
dvdt=F0me−bt
Step 4: Integrate both sides.
To find the velocity, we need to integrate both sides with respect to time t:
∫dv=∫F0me−btdt
The left side integrates to v, and the right side can be integrated using the formula for the integral of an exponential function:
v=F0m∫e−btdt=F0m(−1be−bt)+C
where C is the constant of integration.
Step 5: Determine the constant of integration.
At t=0, the particle is at rest, so v(0)=0:
0=−F0mbe0+C⟹C=F0mb
Step 6: Substitute back to find the expression for velocity.
Now substituting C back into the equation gives:
v(t)=−F0mbe−bt+F0mb
This can be simplified to:
v(t)=F0mb(1−e−bt)
Step 7: Analyze the behavior of the velocity function.
As t→∞, e−bt→0, thus:
v(t)→F0mb
This indicates that the velocity approaches a constant value as time increases.
Conclusion: Identify the correct graph.
The velocity function v(t)=F0mb(1−e−bt) starts at 0 when t=0 and asymptotically approaches F0mb as t increases. This indicates that the graph of v(t) is an increasing function that approaches a horizontal asymptote.
Final Answer:
The correct curve that depicts the speed v(t) is option B.
---
We know from Newton's second law that:
F=m⋅a
where a is the acceleration. Since acceleration can also be expressed as the derivative of velocity with respect to time, we have:
F=m⋅dvdt
Given the force F(t)=F0e−bt, we can substitute this into the equation:
m⋅dvdt=F0e−bt
Rearranging gives us:
dvdt=F0me−bt
To find the velocity, we need to integrate both sides with respect to time t:
∫dv=∫F0me−btdt
The left side integrates to v, and the right side can be integrated using the formula for the integral of an exponential function:
v=F0m∫e−btdt=F0m(−1be−bt)+C
where C is the constant of integration.
At t=0, the particle is at rest, so v(0)=0:
0=−F0mbe0+C⟹C=F0mb
Now substituting C back into the equation gives:
v(t)=−F0mbe−bt+F0mb
This can be simplified to:
v(t)=F0mb(1−e−bt)
As t→∞, e−bt→0, thus:
v(t)→F0mb
This indicates that the velocity approaches a constant value as time increases.
The velocity function v(t)=F0mb(1−e−bt) starts at 0 when t=0 and asymptotically approaches F0mb as t increases. This indicates that the graph of v(t) is an increasing function that approaches a horizontal asymptote.
The correct curve that depicts the speed v(t) is option B.
Topper's Solved these Questions
Similar Questions
A particle of mass m is at rest at the origin at time t=0. It is subjected to a force F(t)=F0e−bt in the X - direction. Its speed V(t) is depicted by which of the following curves.

View SolutionA particle of mass m is at rest at the origin at time t=0 It is subjected to a force F(t)=F0e−bt in the X-direction. Its speed V(t) is depicted by which of the following curves
View Solution
Knowledge Check
A particle of mass m is at rest the origin at time t=0 . It is subjected to a force F(t)=F0e−bt in the x - direction. Its speed v(t) is depicted by which of the following curves ?
A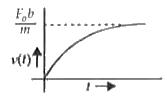 B
B C
C D
D
A block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
A2 FtmB2FtmCFtmDF2t22mA block of mass 2kg is free to move along the x-axis. It at rest and from t=0onwards it is subjected to a time-dependent force F(t) in the x direction. The force F(t) varies with t as shown in the figure. The kinetic energy of the block after 4.5 seconds is
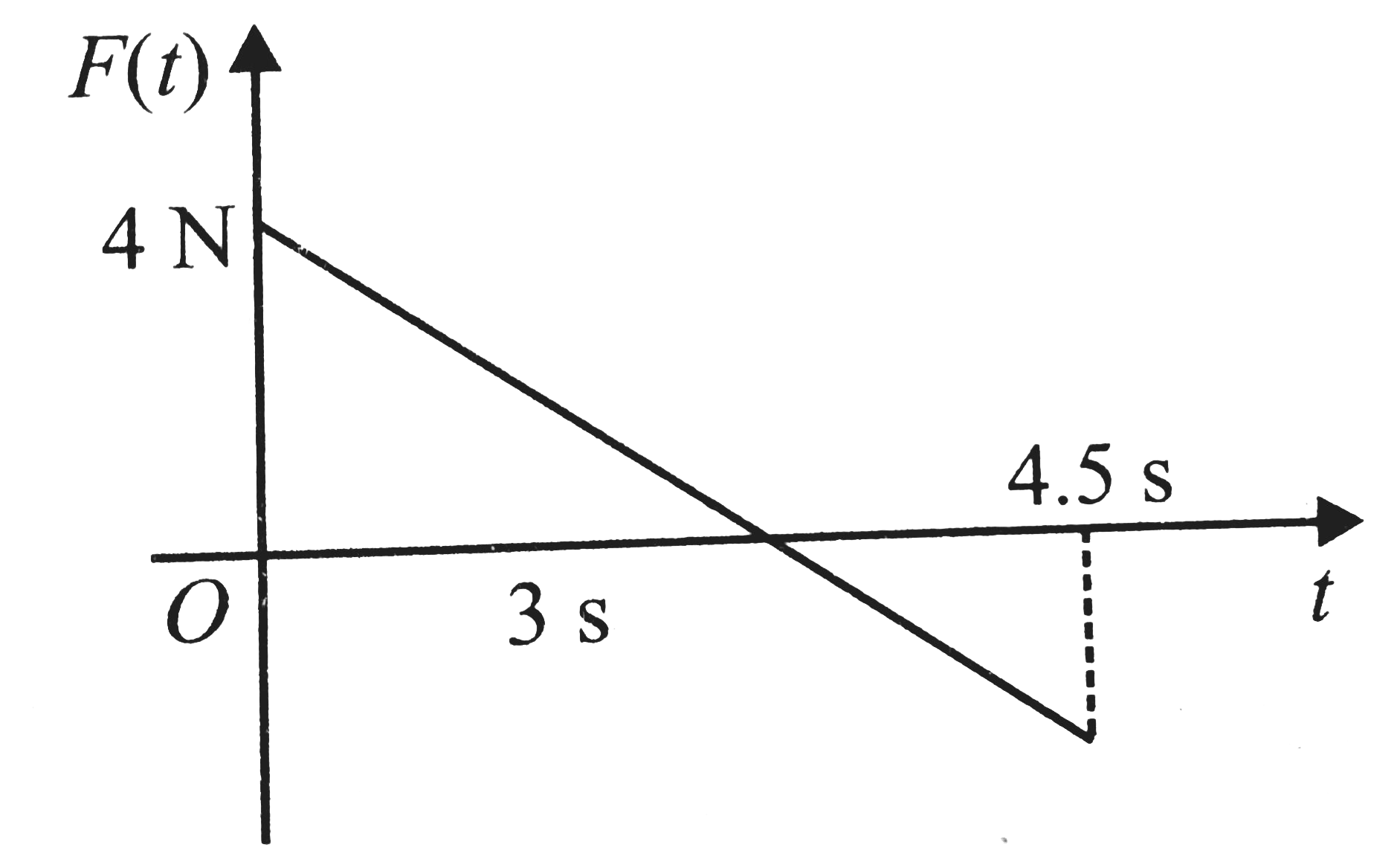 A4.50JB750JC5.06JD14.06J
A4.50JB750JC5.06JD14.06J
A block of mass 2 kg is free to move along the x-axis it is at rset and from t=0 onwards it is subjected to a time dependent force F(t) in the x-direction The force F(t) varies with t as shown in the figure The kinetic energy of the block after 4.5 seconds, is:
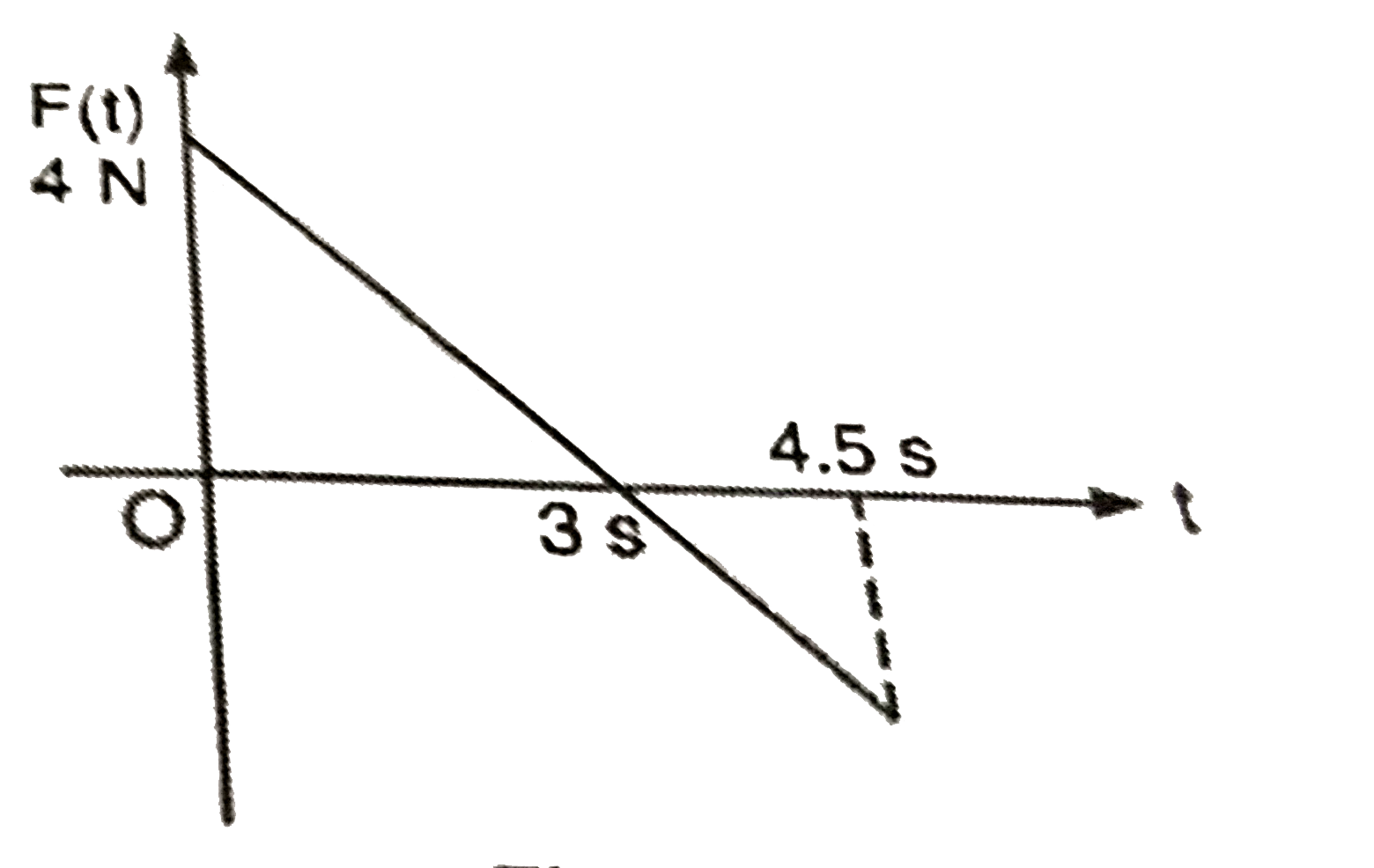
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionAt t=0 aparticle of mass m start moving from rest due to a force →F=F0sin(ωt)ˆi :
View SolutionA particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is
View SolutionA particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is
View Solution

