A cubical block of wood 10 cm on a side and of density 0.5 g/cm3 floats in a jar of water. Oil of density 0.8 g/cm3 is poured on the water until the top of the oil layer is 4 cm below the top of the block. a How deep is the oil layer ?b What is the gauge pressure at the lower face of the block ?
a Let the oil layer be x cm deep. Then weight of block = weight of oil displaced + weight of water displaced.or 103 0.5 = 102 x 0.8 g + 102 6 – x 1or x = 5 cm.b Gauge pressure at the lower face of the block= 5 × 0.8 × 98 + 1 × 1 × 980= 4900 dynes/cm2 .
Related Solutions
A cubical block of wood 10 cm on a side, floats at the interface of oil and water as shown in figure. The density of oil is 0.6 g cm^(-3) and density of water is 1 g cm^(-3) . The mass of the block is
View SolutionA cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
View SolutionA cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
View SolutionA cubical block of wood 10 cm on a side floats at the interface between oil and water with its lower surface horizontal and 4 cm below the interface. The density of oil is . The mass of block is ,
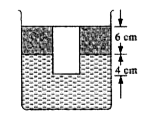
View SolutionA cubical block of wood 10 cm on a side floats at the interface between oil and water with its lower surface horizontal and 4 cm below the interface. The density of oil is 0.6 gcm^(-3) . The mass of block is
View SolutionA cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is

View SolutionA cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is 0.6g cm^(-3) and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is
View SolutionA cubical block of wood along each side floats at the interface between an oil and water with its lowest surface below the interface. If the height of oil and water columns are each and find a the mass of the block, b. the liquid pressure at the lower surface of the block.
View SolutionA cubical block of wood 10 cm along each side floats at the interface between an oil and water with its lowest surface 2cm below the interface. If the height of oil and water columns are 10 cm each and rho_("oil")=0.8g/"cc", find a the mass of the block, b. the liquid pressure at the lower surface of the block.
View SolutionA cubical block of wood of side 10 cm floats at the interface between an oil and water with its lower surface 2 cm below the interface. the heights of the oil and water columns are 10 cm each. Density of oil is 0.8g/c.c. The mass of the block is
View SolutionA cubical block of wood of side 10 cm floats at the interface between an oil and water with its lower surface 2 cm below the interface. the heights of the oil and water columns are 10 cm each. Density of oil is 0.8g/c.c. The mass of the block is
View SolutionA cubical block of wood of side 10 cm floats at the interface between an oil and water with its lower surface 2 cm below the interface. The heights of the oil and water columns are 10 cm each. Density of oil is 0.8g/c.c. The mass of the block is
View SolutionA cubical block of wood on a side floats at the interface between oil and water, as in fig. with its lower face below the interface. The intensity of the oli is . The mass of the block is

View SolutionA cubical block of wood, of length 10 cm, floats at the interface between oil of density and water. The lower surface of the block is 1.5 cm below the interface. If the depth of water is 10 cm below the interface and oil is upto 10 cm above the interface then the difference in pressure at the lower and the upper face of the wooden block is (Assume density of water ) and acceleration of gravity , )
View SolutionA block of wood floats in fresh water with two-thirds of its volume sinking. In oil, the block floats with one-fourth of its volume sinking. is the density of the oil
View SolutionA cubical block of wool of side 10 cm floats at the interface between an oil and water with its Jower surface 2cm below the interface, the heights of the oil and water columns are 10 cm each Density of oil ist) Spec. The mass of the block is
View SolutionA cubical block of wood of 10cm and mass 0.92kg floats on a tank of water with oil or rel. density 0.6 . Thickness of oil is 4cm above water. When the block attains equilibrium with four of its sides edges verical:
View Solution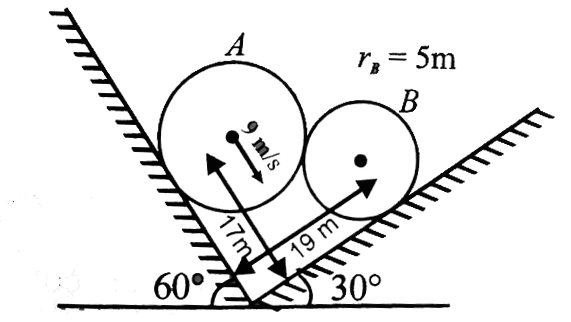
System is shown in the figure. Velocity of sphere A is 9 . Find the speed of sphere B.
View SolutionA layer of oil with density 724 kg floats on water of density . A block floats on the oil-water interface with of its volume in oil and of its volume in water, as shown in the figure. What is the density of the block?

View SolutionA wooden cube with a side of 10 cm whose mass is 0.92 kg is floating in an oily water. The relative density of the oil is 0.6 and the surface of the oil is 4 cm above the water when the block is in equilibrium.
View Solution