The figure below shows a bead sliding down a frictionless wire from point P to point Q. The brachistochrone problem asks what shape the wire should be in order to minimize the bead’s time of descent from P to Q. In June of 1696 John Bernoulli proposed this problem as a public challenge with a 6-month deadline later extended to Easter 1697 at George Leibniz’s request. Isaac Newton then retired from academic life and serving as Warden of the Mint in London received Bernoulli’s challenge on January 29 1697. The very next day he communicated his own solution - the curve of minimal descent time is an arc of an inverted cycloid - to the Royal Society of London. For a modern derivation of this result suppose the bead starts from rest at the origin P and let y=yx be the equation of the desired curve in a coordinate system with the y-axis pointing downward. Then a mechanical analogue of Snell’s law in optics implies thatwhere c denotes the angle of deflection from the vertical of the tan gent line to the curve - so cotα=y’x why? - and u=√2gh is the bead’s velocity when it has descended a distance y vertically from KE =1/2 mv2 = mgy = -PE. First derive from sinα/u = constant the differential equationwhere a is an appropriate positive constant.
Denote the constant sinα/v with the letter C. Then as we have:Now v = √2gy so this equals:
Related Solutions
In comparing the resistance of two cells P and Q with a sides wire bridge, a balance point is obtained when the sliding contact is 30 cm from the zero end of the wire. The resistances P and Q are interchanged and the balance is obtained at 120 cm from the same emf. Find the ratio of the resistance P and Q and the length of the bridge wire
View SolutionIn comparing the resistance of two cells P and Q with a sides wire bridge, a balance point is obtained when the sliding contact is 30 cm from the zero end of the wire. The resistances P and Q are interchanged and the balance is obtained at 120 cm from the same emf. Find the ratio of the resistance P and Q and the length of the bridge wire
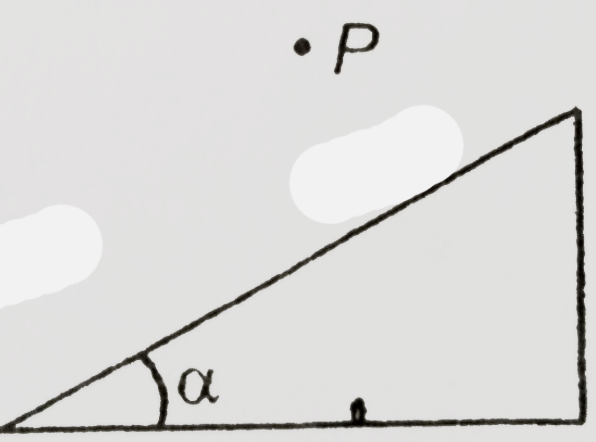
View SolutionA point P is located above an inclined plane. It is possible to reach the plane by sliding under gravity down a straight frictionless wire joining to some point P on the plane. How should P be chosen so as to minimize the time taken ?
View Solutionएक लम्बे क्षैतिज तार P में 50 ऐम्पियर की धारा है। यह तार दृढ़तापूर्वक स्थिर है। एक-दूसरे पतले तार Q को तार P के ठीक ऊपर तथा उसके समान्तर रखा जाता है । तार Q का भार न्यूटन/मीटर है तथा इसमें 25 ऐम्पियर की धारा है। तार A की तार P से वह दुरी ज्ञात कीजिये । जिस पर तार Q चुंबकीय प्रतिकर्षण-बल के कारण स्थिर रहे। तार P के सापेक्ष तार Q में धारा की दिशा भी बताइए। न्यूटन/ऐम्पियर
View Solution1 m long metallic wire is broken into two unequal parts P and Q. P part of the wire is uniformly extended such that the wire has twice the length of P and its resistance is equal to Q. Find the ratio of resistances P and R where R is the name ofthe extended wire and ratio of length P and Q.
View Solution1 m long metallic wire is broken into two unequal parts P and Q. P part of the wire is uniformly extended such that the wire has twice the length of P and its resistance is equal to Q. Find the ratio of resistances P and R where R is the name of the extended wire and ratio of length P and Q.
View SolutionA 2m long metallic wire is broken into two unequal points P and Q. P part of the wire is uniformly extended into another wire R. Length of R is twice the length of P and resistance of R is equal to that of Q. Find the ratio of resistances of P and R and also the ratio of lengths of P and Q.
View SolutionA bead of mass m can side on a frictionless wire as shown in figure Bacause of the given shape of the wire near p the bottom point , it can be approximatedd as abola near p the potential energy of the bead is given U = cx^(2) where c is a constant and x is measured from p The bead if displacvement slighly from point p will oscillate about p The period of oscillation is
View SolutionIf the points (p, q) and (q, p) are equidistant from the point (x, y). show that x = y.
View SolutionA bead is free to slide down on a smooth wire rightly stretched between points A and B on a vertical circle of radius 10 m . Find the time taken by the bead to reach point B , if the bead slides from rest from the highest point A on the circle. .
View SolutionA bead is free to slide down on a smooth wire rightly stretched between points A and B on a vertical circle of radius 10 m . Find the time taken by the bead to reach point B , if the bead slides from rest from the highest point A on the circle. .
View Solutionबिंदुओं P(2,3,5) और Q(-1,2,4) से होकर जाने वाली रेखा की दिक्कोज्याएँ ज्ञात कीजिए |
View SolutionIf one mole of electrons is passing from point P to another point Q on a straight metal wire in time interval of 1 ms, then what will be the magnitude of current in the wire ? What is the direction of current ?
View SolutionA bead is free to slide down a smooth wire tightly stretched between points A and B on a vertical circle. If the starts from rest at A , the heighest point on the circle
View Solutionବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନୋତ୍ତର ।
ରୂପଟି କେତେ ?
View SolutionA long horizontal wire carries of . It is rigidly fixed. Another fine wire is placed directly above and parallel to . The wieght of wire is and carries a current of . Find the position of wire from so that the wire remains suspended due to magnetic repulsion.
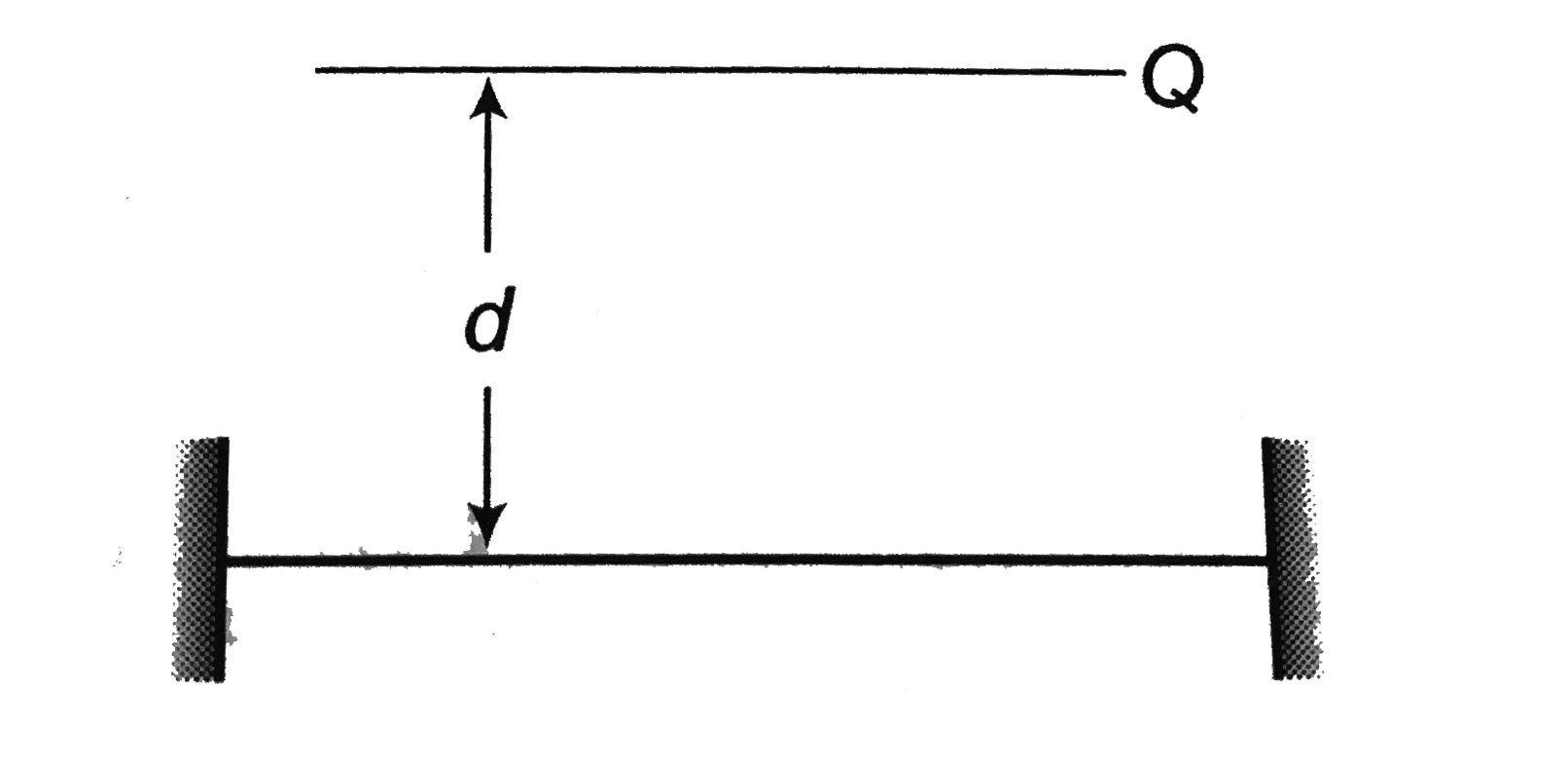
View SolutionA long horizontal wire P carries of 50 A . It is rigidly fixed. Another fine wire Q is placed directly above and parallel to P . The wieght of wire Q is 0.075 N//m and carries a current of 25 A . Find the position of wire Q from P so that the wire Q remains suspended due to magnetic repulsion.
View SolutionA wire which is bent in the shape of a curve given by, . A bead of mass m is located at point P(x,y). If the wire is smooth, find with which wire needs to be rotated for bead to be static.
View SolutionA wire which is bent in the shape of a curve given by, . A bead of mass m is located at point P(x,y). If the wire is smooth, find with which wire needs to be rotated for bead to be static.
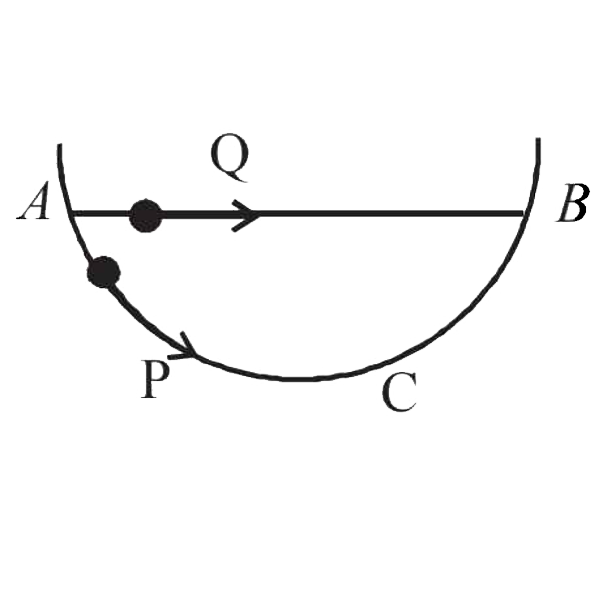
View SolutionA particle P is sliding down a frictionless hemispherical bowl. It passes the point A at . At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at along the horizontal string AB, with the speed v. Friction between the bead and the string may be neglected. Let and be the respective times taken by P and Q to reach the point B. Then:
View Solution