Figure shows two sphere of mass M each S1 and S2 .Alight rigid rod has two lead balls each of mass m. The rigid rod is suspended from vertical wire.S1 pulls A and S2 pulls B so that the rod turns by θ. The twist in suspension wire is producing a restoring torque.If AS1 = BS2 = d determine the torisonal constant of suspension fibre S. Find its order if G = 6.67 × 10 –11 Nm2 kg –2 m M ~ 102 kg L ~ 1 m and d ~ 1 mm.
Torque due to gravitational forces on A and on B isThis must be balanced by the restoring torque τ´ = cθ.
Related Solutions
Two small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle and released. Find the tension in the rod as the system passes through the mean position.
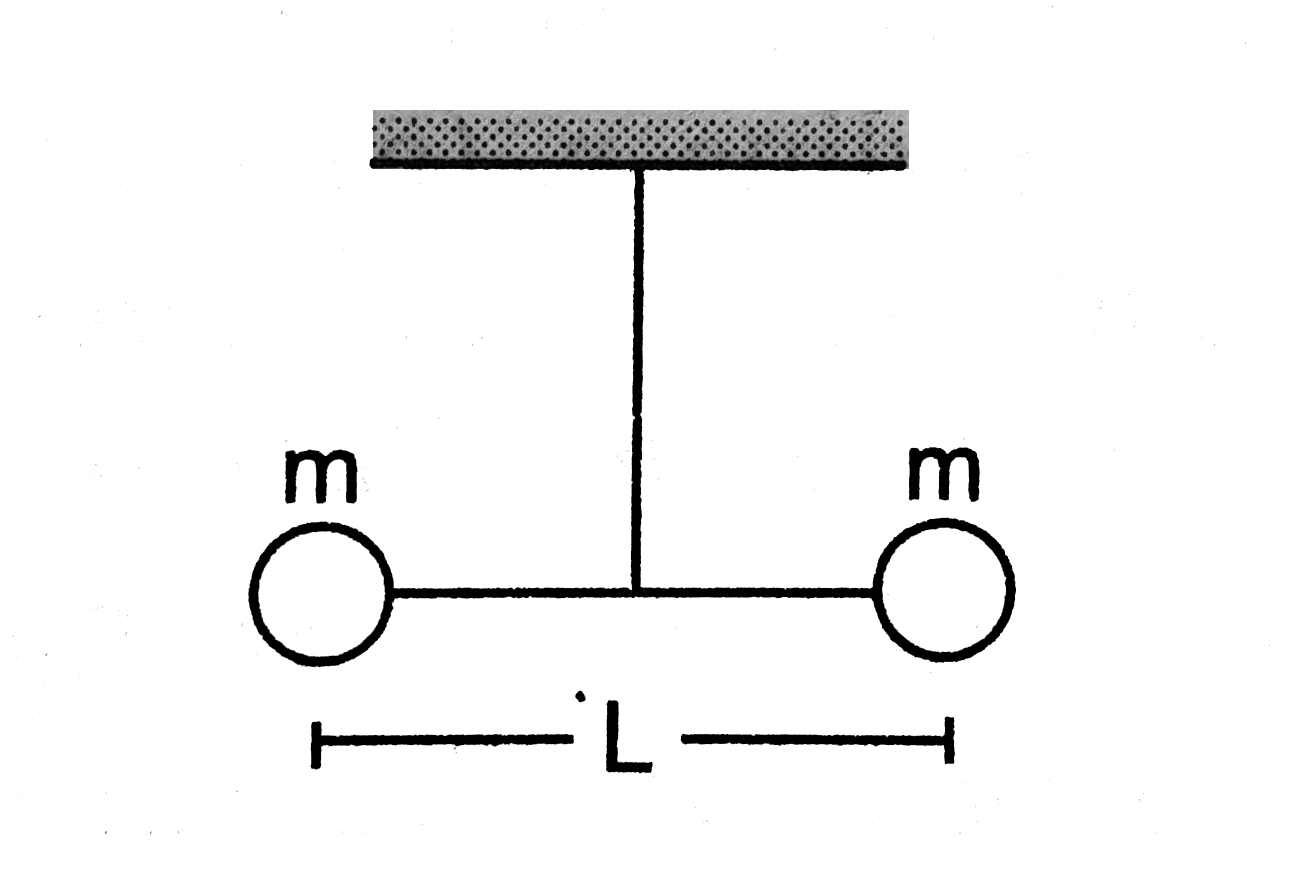
View SolutionTwo small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle and released. Find the tension in the rod as the system passes through the mean position.

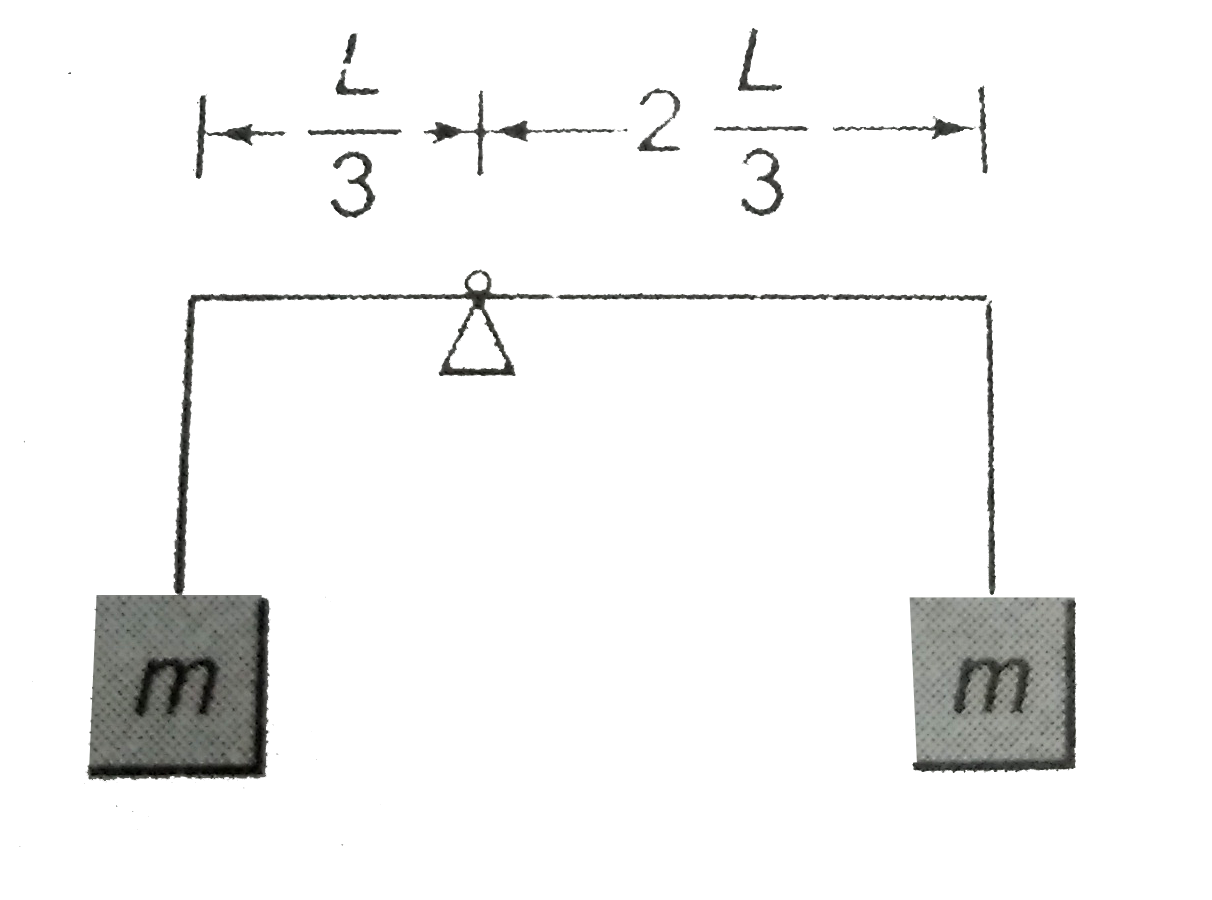
View SolutionAs shown in the figure, two blocks, each of mass , suspended from the ends of a rigid light rod of length . The rod is held horizontally on the fulcrum and then released.
() Find the initial angular acceleration of the rod.
() If the mass of rod is also uniformly distributed. find the tension in the strings attached to blocks.
View SolutionThe figure shows the line of symmetry of the Cavendish experiment, to determine the value of the gravitational constant, two lead balls are placed at the ends of the rod AB and the rod is suspended from a rigid end by a net wire. Two large lead balls are brought near the smaller one, but are shown in opposite directions The resultant moment on the rod is
View SolutionThe figure shows the line of symmetry of the Cavendish experiment, to determine the value of the gravitational constant, two lead balls are placed at the ends of the rod AB and the rod is suspended from a rigid end by a net wire. Two large lead balls are brought near the smaller one, but are shown in opposite directions The resultant force on the rod is
View SolutionA rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.
View SolutionA rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.

View SolutionTwo blocks of masses 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 m. The upper wire has negligible mass and the lower wire has a uniform mass of 0.2 kg/m. Thewhole system of block, wire and support have an upward acceleration of 0.2 m/s2. g = 9.8 m/s2. The tension at the mid-point of lower wire is-

View SolutionTwo blocks of masses 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 m. The upper wire has negligible mass and the lower wire has a uniform mass of 0.2 kg/m. Thewhole system of block, wire and support have an upward acceleration of 0.2 m/s2. g = 9.8 m/s2. The tension at the mid-point of lower wire is-

View SolutionTwo blocks of masses 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 m. The upper wire has negligible mass and the lower wire has a uniform mass of 0.2 kg/m. Thewhole system of block, wire and support have an upward acceleration of 0.2 m/s2. g = 9.8 m/s2. The tension at the mid-point of lower wire is-

View SolutionA conducting rod of length 1 m and mass 1 kg is suspended by two vertical wires through its ends. An external magnetic field 2 T is applied normal to the rod. Now find the current flowing through the rod, so that the tension in the wires becomes zero. [g = 10 "m s"^(-2)]
View SolutionTwo masses m and (m)/(2) are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is tau=ktheta for angular displacement theta . If the rod is rotated by theta_(0) and released, the tension in it when it passes through its mean position will be :
View SolutionTwo masses m and (m)/(2) are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is tau=ktheta for angular displacement theta . If the rod is rotated by theta_(0) and released, the tension in it when it passes through its mean position will be :
View SolutionOne end of a uniform rod of mass M and cross sectional area A is suspended from rigid support and an equal mass M is suspended from the other end . The stress at the midpoint of the rod will be
View SolutionOne end of a uniform rod of mass M and cross- sectional area A is suspended from rigid support and an equal mass M is suspended from the other end. The stress at the mid point of the rod will be
View SolutionOne end of a uniform rod of mass M and cross-sectional area A is suspended from a rigid support and an equal mass M is suspended from the other end, what is the stress at the mid point of the rod.
View Solutionदो द्रव्यमान, प्रत्येक m, को मध्य बिन्दु B तथा अंतिम बिन्दु C पर संयोजित है, द्रव्यमान हीन छड़ AC, A से लटका हुआ है। यह चित्र में दर्शाए अनुसार क्षैतिज स्थिति से मुक्त किया जाता है। हिंज (hinge)A पर बल जब छड़ उधिर होती है, ज्ञात कीजिये।
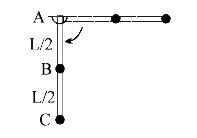
View Solutionदो गोले, जिनमें प्रत्येक का द्रव्यमान 1 किग्रा है, 2 मीटर लम्बी छड़ के दोनों सिरों से जुड़े हैं। छड़ का द्रव्यमान तथा गोलों का आकार नगण्य है। निकाय का छड़ की लम्बाई के लम्बवत्-
द्रव्यमान केन्द्र
View SolutionA cylindrical rod of mass 'm' length L and radius 'R' has two cords wound around it whose ends are attached to a rigid support. The rod is held horozontally with the two cords vertical. When the rod is released, the cords unwind and rod rotates. Find the tension in the cords as they unwound and determine the linear acceleration of the cylinder as it falls.
View SolutionA cylinderical rod of mass .m. length L and radius .R. has two cords wound around it whose ends are attached to a rigid support. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and rod rotates. Find the tension in the cords as they unwound and determine the linear accelerations of the cylinder as it falls.
View Solution