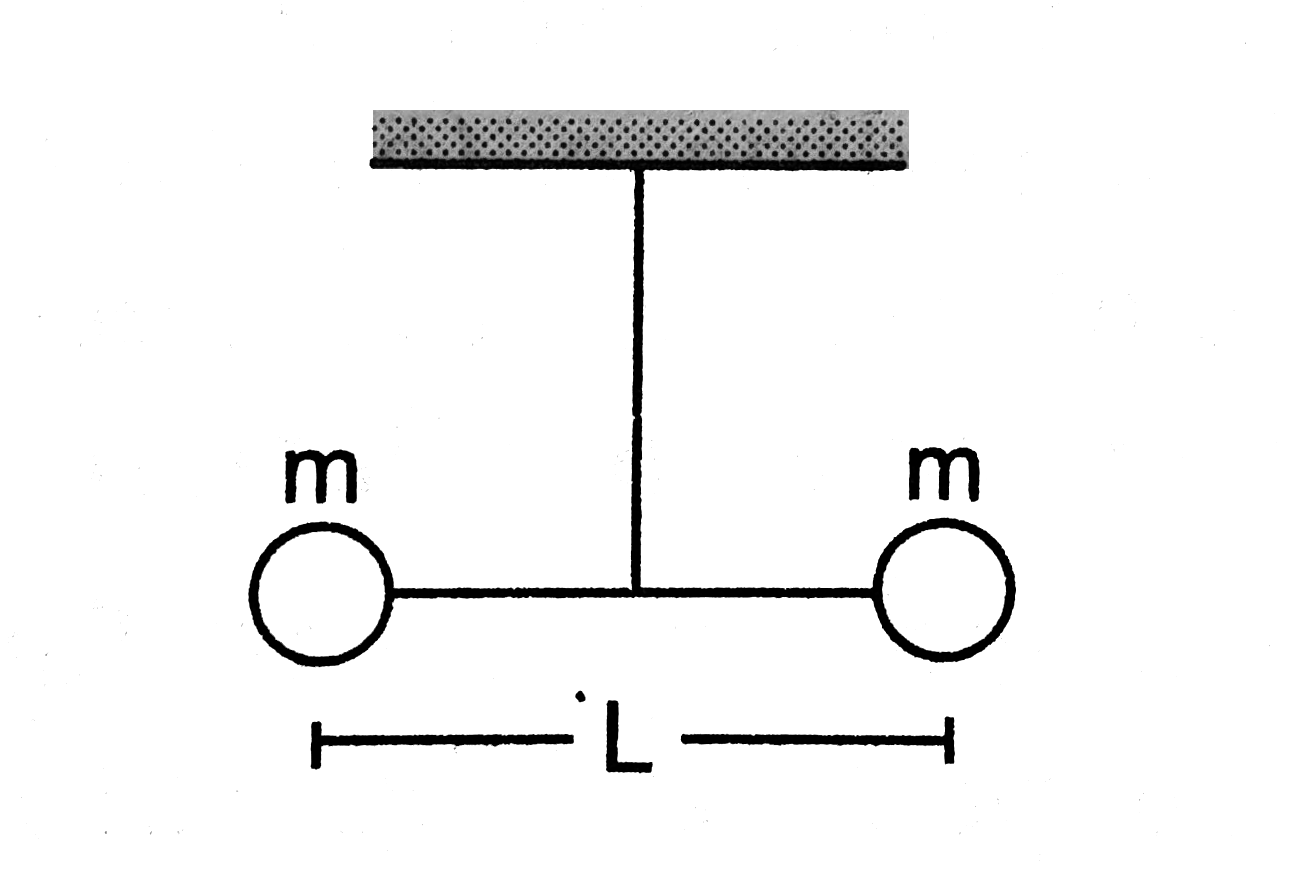
Two small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B, D
The M.I. of the two ball system
I=2m(L2)2=mL22

At any position θ during the oscillation
→rque=kθ
So, work done during the displacement 0→θ0.
ω=∫θ00kθdthη=kθ202
By work energy method
12Iω2−0=workdo≠=kθ202
∴=kθ2I=kθ20mL2

Now from the free body diagram of the rod
T2=√(mω2L)2+(mg)2
=√mkθ20mL2×L2⎞⎟⎠+m2g2
=⎛⎜
⎜⎝√k2θ20L2+m2g2⎞⎟
⎟⎠
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
16 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Select the correct statements
View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
View SolutionA load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
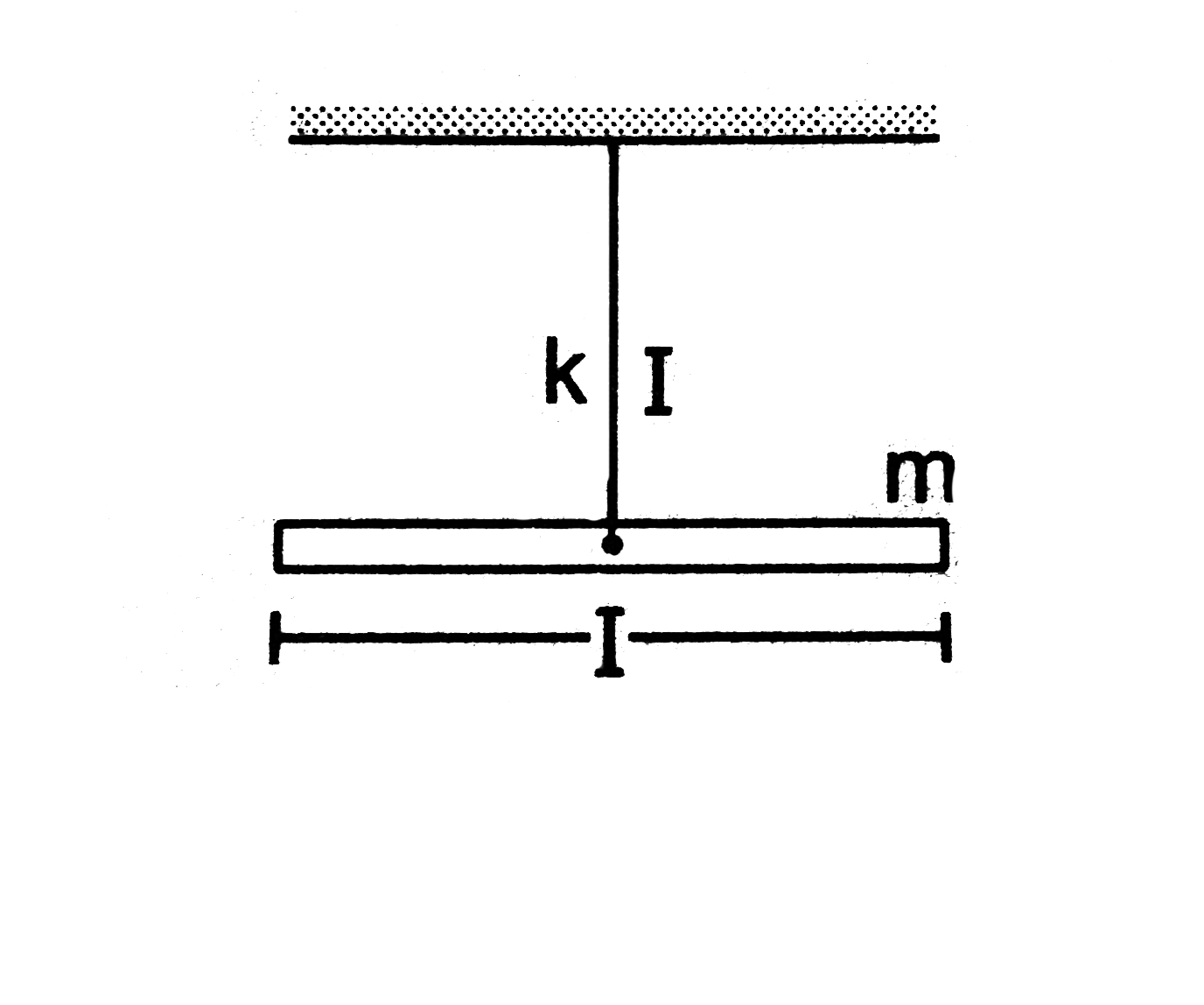
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.
View SolutionTwo masses m and (m)/(2) are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is tau=ktheta for angular displacement theta . If the rod is rotated by theta_(0) and released, the tension in it when it passes through its mean position will be :
View Solutionचित्र 22.5 में द्रव्यमान m एवं लम्बाई l वाली एक समरूप छड़ को लम्बाई l वाले पतले तथा नगण्य भार वाले तार द्वारा लटकाया गया है। तार का मरोड़ी नियतांक k है। आवर्तकाल ज्ञात कीजिए यदि (a) छड़ ऊर्ध्वाधर तल में निलंबन-बिंदु के पारित: छोटे दोलन करती है (b) छड़ क्षैतिज तल में अपने केंद्र के पारित: छोटे दोलन करती है।

View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.

View SolutionTwo masses m and (m)/(2) are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is tau=ktheta for angular displacement theta . If the rod is rotated by theta_(0) and released, the tension in it when it passes through its mean position will be :
View SolutionFind the moment of inertia of thin and massless rod about an axis passing through its centre of mass of rod and pair of mass is suspended on both end of this rod.
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View SolutionTwo particles each of mass m and charge q are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo particles, each of mass m and charge q are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through ts centre. Find the ratio of the magnetic moment of the system and its angular momentum about the axis through the centre of the rod.
View Solution
