A particle of mass M is elastically scattered from a stationary proton of mass m. The proton is projected at an angle ϕ = 22.1◦ while the incident particle is scattered through an angle θ = 5.6◦ with the incident direction. Calculate M in atomic mass units. This event was recorded in photographic emulsions in the Wills Lab. Bristol.
We shall find an expression for the ratio of the masses M/m in terms of the angles θ and ϕ. To this end we start with the equation for the transformation of angle from CMS to LS. tan θ = sin θ∗/cosθ∗ + M/m 1 θ∗ = π − ϕ∗ = π − 2ϕbecause m and M are oppositely directed in the CMS and the recoil angle of the proton in the CMS is always twice the angle in the LS Therefore sinθ∗ = sinπ − 2ϕ = sin2ϕ and cosθ∗ = cosπ − 2ϕ = − cos2ϕ Equation 1 then becomes tanθ = sinθ/ cosθ = sin2ϕ/M/m − cos 2ϕ Cross multiplying the second equation and re-arranging M/m sinθ = sinθcos2ϕ + cosθsin2ϕ = sinθ + 2ϕ M/m = sinθ + 2ϕ/ sinθ Using θ = 5.60 and ϕ = 22.10 we find M = 7.8 m ≈ 7.8 amu.
Related Solutions
A partical of mass moving with velocity collides perfectly elastically with another particle of mass . If the incident particle is deflected by . The heavy mass will make and angle with the initial direction of equal to:
View SolutionA proton of mass m collides elastically with a particle of unknown mass at rest After the collision the proton and the unknwon particle are seen moving at an angle fo with respect to each other The mass of unknown particle is :
View SolutionA proton of mass m collides elastically with a particle of unknown mass at rest After the collision the proton and the unknwon particle are seen moving at an angle fo 90^(@) with respect to each other The mass of unknown particle is :
View SolutionA particle of mass m has a velocity of 1 m s^(-1) , which makes a perfectly elastic collision with another stationary particle of mass 2 m. If, the incident particle 90^@ is deflected by. A heavy mass m makes an angle A with the initial direction, that is equal to:
View SolutionA partical of mass moving with velocity collides perfectly elastically with another particle of mass . If the incident particle is deflected by . The heavy mass will make and angle with the initial direction of equal to:
View SolutionA partical of mass moving with velocity collides perfectly elastically with another particle of mass . If the incident particle is deflected by . The heavy mass will make and angle with the initial direction of equal to:
View SolutionA particle of mass m collides with a stationary particle and continues to move at an angle of with respect to the original direction . The second particle also recoils at an angle of to this direction . The mass of the second particle is (collision is elastic )
View SolutionA particle of mass m collides with a stationary particle and continues to move at an angle of 45^(@) with respect to the original direction. The second particle also recoils at an angle of 45^(@) to this direction. The mass of the second particle is (collision is elastic)
View Solutionएक m द्रव्यमान का अल्फ़ा कण किसी अज्ञात द्रव्यमान के स्थिर नाभिक से एक-विमीय प्रत्यास्थ संघट्ट करके अपनी प्रारम्भिक गतिज ऊर्जा का 64% भाग क्षय करके ठीक विपरीत दिशा में प्रकीर्णित हो जाता है। नाभिक का द्रव्यमान होगा
View SolutionA particle of mass M strikes a wall at an angle of incidence with velocity V elastically Then the change in momentum is
View SolutionA particle of mass m strikes elastically against a wall at angle of incidence with velocity v. The change momentum is
View SolutionA particle of mass m strikes elastically against a wall at angle of incidence with velocity v. The change in momentum is
View SolutionA particle of mass moving with some velocity on a smooth surface strikes another particle of mass at rest , elasticity head - on. What fraction of incident is transferred to the particle of mass .
View SolutionFind the greatest possible angle through which a deuteron is scattered as result of elastic collision with an initially stationary proton ? Take m_(1) & m_(2) as masses of a proton & a deuterium.
View SolutionFind the gratest possible angle through which a deutron is scattered as a result of elastic collision with an initially stationary proton.
View SolutionA particle of mass m and veocity collides elastically with a stationary particle of mass m Calculate the angle between velocity vector of the two partiicless after the collision.
View SolutionA particle of mass m having collides with a stationary particle of mass M deviated by an angle whereas the particle M recoiled at an angle to the direction of theinitial motion of the particle m. How much in percent and in what way has the kinetic energy of this system changed after the collision, if .
View SolutionA particle of mass m having collided a stationary particle of mass M deviated by an angle whereas the particle M recoiled at an angle to the direction of the initial motion of the particle m. How much in percent and in what way has the kinetic energy of this system changed after the collision, if M/m = 5 ?
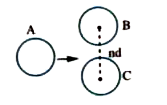
View SolutionA relativistic proton with kinetic energy K collides with a stationary proton. Assuming the collision to he elastic and the energy to be partitioned equally between the particles, find the scattering angle. Calculate for the cases K = = 500 MeV and K = 10 GeV.
View Solutionm द्रव्यमान का एक कण M द्रव्यमान के स्थिर कण पर टकराता है। यदि संघट्ट के पश्चात् m कण रुक जाता है, तब संघट्ट (प्रत्यास्थता) गुणांक होगा
View Solution