A partical of mass m moving with velocity 1m/s collides perfectly elastically with another particle of mass 2m. If the incident particle is deflected by 90∘. The heavy mass will make and angle θ with the initial direction of m equal to:
60∘
45∘
15∘
30∘
The correct Answer is:D
From coservation of momentum along incident direction
m×1=2mv2cosθ…….i
From conservation of momentum along perpendicular direction,
m×0+2m×0=mv1−2mv2sinθ
⇒v1=2v20sinθ…………ii
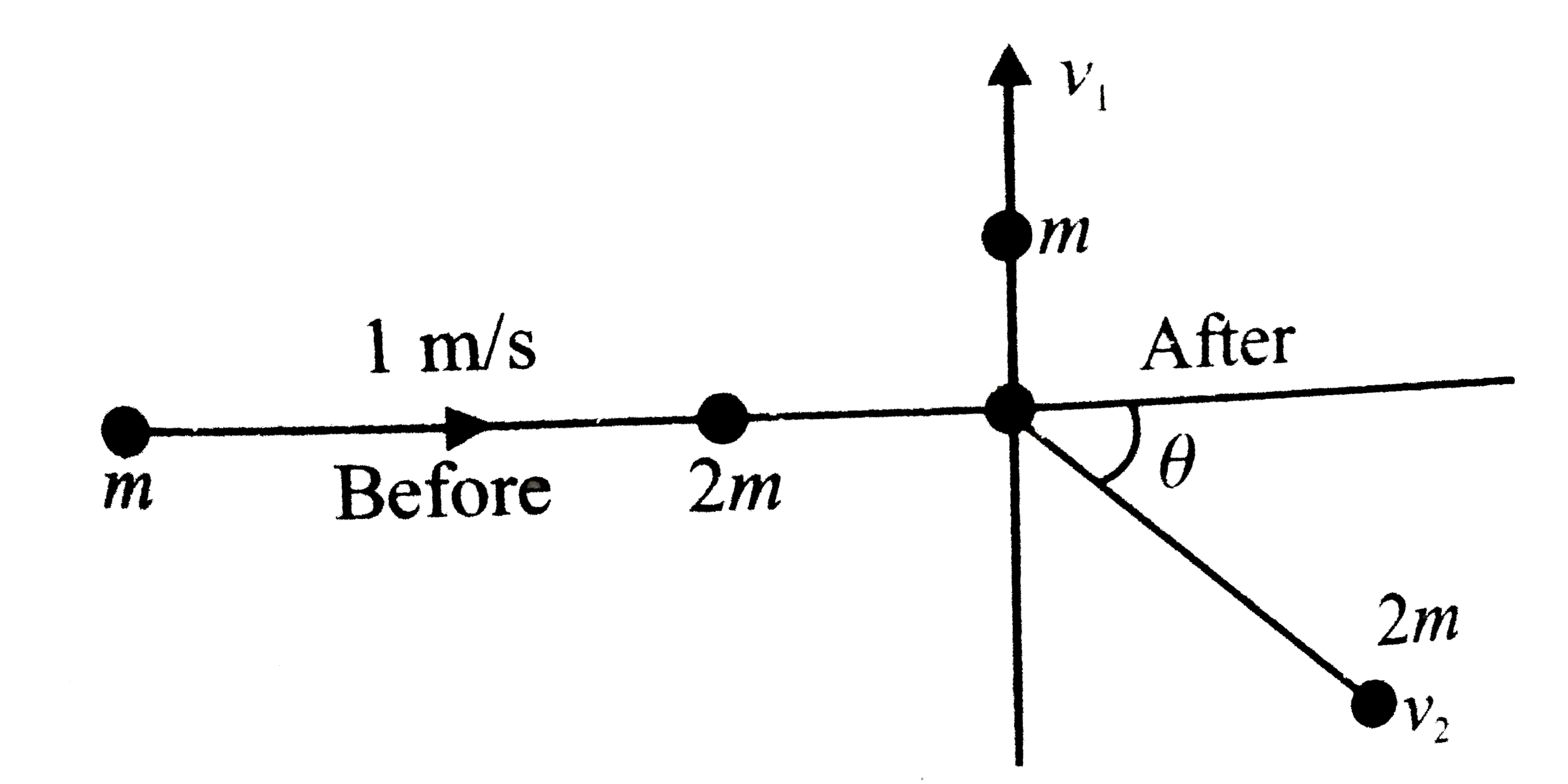
From energy conservartion
12m×(1)2=12mv21+122mv22.......iii
From eqn i, ii and iii we get θ=306∘
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Multiple Correct
Explore 25 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Subjective
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View Solution
Knowledge Check
A partical of mass m moving with velocity 1m/s collides perfectly elastically with another particle of mass 2m. If the incident particle is deflected by 90∘. The heavy mass will make and angle θ with the initial direction of m equal to:
A60∘B45∘C15∘D30∘A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
A34μ2B38μ2C14μ2D18μ2A particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
Av3B−v3C2v3D−2v3
A particle of mass m1 moves with velocity v1 and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is
View SolutionA body of mass m2 moving with velocity v0 collides elastically with another mass of m3 . Find % change in KE of first body
View SolutionA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
View SolutionA particle of mass m1=4kg moving at 6ˆims−1perfectly elastically with a particle of mass m2=2 moving at 3ˆims−1
View SolutionTwo particles of same mass m moving with velocities u1 and u2 collide perfectly inelastically. The loss of energy would be :
View Solution

