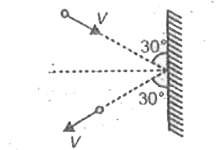
A particle of mass M strikes a wall at an angle of incidence 60∘ with velocity V elastically Then the change in momentum is
MV2
MV
−2MV
zero
The correct Answer is:B
To find the change in momentum of a particle of mass M striking a wall at an angle of incidence 60∘ with velocity V elastically, we can follow these steps:
Step 1: Understand the scenario
The particle strikes the wall at an angle of 60∘. In an elastic collision, the angle of incidence is equal to the angle of reflection. Therefore, the particle will leave the wall at the same angle 60∘ after the collision.
Step 2: Resolve the velocity into components
The initial velocity V can be resolved into two components:
- The horizontal (x-axis) component:
Vx=Vcos(60∘)=V⋅12=V2
- The vertical (y-axis) component:
Vy=Vsin(60∘)=V⋅√32
Step 3: Calculate initial momentum
Before the collision, the momentum in the x-direction and y-direction can be calculated as follows:
- Initial momentum in the x-direction:
Pix=MVx=M⋅V2=MV2
- Initial momentum in the y-direction:
Piy=MVy=M⋅V⋅√32=MV√32
Step 4: Calculate final momentum after collision
After the collision, the x-component of the velocity will be in the opposite direction, while the y-component remains the same:
- Final momentum in the x-direction:
Pfx=M(−Vx)=M(−V2)=−MV2
- Final momentum in the y-direction:
Pfy=MVy=M⋅V⋅√32=MV√32
Step 5: Calculate change in momentum
Now we can calculate the change in momentum for both x and y directions:
- Change in momentum in the x-direction:
ΔPx=Pfx−Pix=−MV2−MV2=−MV
- Change in momentum in the y-direction:
ΔPy=Pfy−Piy=MV√32−MV√32=0
Step 6: Final result
The total change in momentum is primarily in the x-direction because the y-direction momentum remains unchanged. Therefore, the change in momentum is:
ΔP=ΔPx=−MV
Summary
The change in momentum of the particle after striking the wall is −MV in the x-direction, and there is no change in the y-direction.
---
The particle strikes the wall at an angle of 60∘. In an elastic collision, the angle of incidence is equal to the angle of reflection. Therefore, the particle will leave the wall at the same angle 60∘ after the collision.
The initial velocity V can be resolved into two components:
- The horizontal (x-axis) component:
Vx=Vcos(60∘)=V⋅12=V2
- The vertical (y-axis) component:
Vy=Vsin(60∘)=V⋅√32
Before the collision, the momentum in the x-direction and y-direction can be calculated as follows:
- Initial momentum in the x-direction:
Pix=MVx=M⋅V2=MV2
- Initial momentum in the y-direction:
Piy=MVy=M⋅V⋅√32=MV√32
After the collision, the x-component of the velocity will be in the opposite direction, while the y-component remains the same:
- Final momentum in the x-direction:
Pfx=M(−Vx)=M(−V2)=−MV2
- Final momentum in the y-direction:
Pfy=MVy=M⋅V⋅√32=MV√32
Now we can calculate the change in momentum for both x and y directions:
- Change in momentum in the x-direction:
ΔPx=Pfx−Pix=−MV2−MV2=−MV
- Change in momentum in the y-direction:
ΔPy=Pfy−Piy=MV√32−MV√32=0
The total change in momentum is primarily in the x-direction because the y-direction momentum remains unchanged. Therefore, the change in momentum is:
ΔP=ΔPx=−MV
The change in momentum of the particle after striking the wall is −MV in the x-direction, and there is no change in the y-direction.
Topper's Solved these Questions
- LAWS OF MOTION, FRICTION AND ARCHIMEDES' PRINCIPLEBOOK - MCGROW HILL PUBLICATIONCHAPTER - LAWS OF MOTION, FRICTION AND ARCHIMEDES' PRINCIPLEEXERCISE - HIGHER ORDER THINKING QUESTIONS
34 Videos
- HEATING AND MAGNETIC EFFECTS OF CURRENT BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEATING AND MAGNETIC EFFECTS OF CURRENT EXERCISE - HIGHER ORDER THINKING QUESTIONS
34 Videos
- MEASUREMENTBOOK - MCGROW HILL PUBLICATIONCHAPTER - MEASUREMENTEXERCISE - ELEMENTARY QUESTIONS (HIGHER ORDER THINKING QUESTIONS)
13 Videos
Similar Questions
A particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
View SolutionA particle of mass m is strikes on ground at an angle of incidence 30∘ with initial speed of 5 m/s . Calculate (i) its velocity after impact (ii) angle of reflection . Given that the coefficient of restitution is 1√3
View Solution
Knowledge Check
A particle of mass m strikes elastically against a wall at angle of incidence 60∘ with velocity v. The change in momentum is
AmvB2mvCmv2Dmv4A particle of mass, strikes on ground with angle of incidence 45∘, what will be the velocity after reflection if coefficient of restitution e=1√2
A√2v3Bv√3Cv2D√3v2A partricle of mass m is projected with a velocity v at an angle of 60∘ with horizontal When the particle is at the maximum height. The magnitude ofits angular momentum about the point ofprojection is
AzeroB3mv216gC√3mv316gD3mv316g
A particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View SolutionA particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
View SolutionA particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.

View SolutionA body of mass m is projected with velocity v at an angle of 45∘ with the horizontal. Find the change in its momentum at the end of flight.
View SolutionA jet of water with cross section of 6cm2 strikes a wall at an angle of 60∘ to the normal and rebounds elastically from the wall without losing energy. If the velocity of the water in the jet is 12m/s, the force acting on the wall is
View Solution
