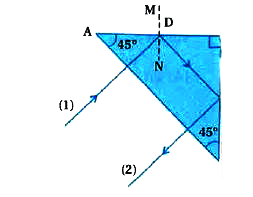
Two orthogonally polarized beams each of wavelength 0.5 μm and with polarization marked in the figure are incident on a two-prism assembly and emerge along x -direction as shown. The prisms are of identical material and n0 and ne are the refractive indices of the o -ray and e -ray respectively. Usesinφ = sinθ/3 and n0 = √3 + 1/4a Find the value of θ and ne .b If the right hand side prism starts sliding down with the vertical component of the velocity uy = 1μm/s what would be the minimum time after which the state of polarization of the emergent beam would repeat itself?
a The beam will propagate as an o − ray in the first prism because the vibrations are perpendicular to the optic axis and will see the refractive index n0 . When this beam enters the second prism it will become an e− ray and will see the refractive index ne . For calcite no > ne and the ray will bend away from the normal. Since the optic axis is normal to the plane of the refracted ray will obey Snell’s laws and the angle of refraction will be given by no sin30° = ne sinθWe next consider the incidence of a second beam. The beam will propagate as an e − ray in the first prism and as an o −ray in the second prism. The angle of refraction is nowb The state of polarization will repeat if change in phase difference δ is π . The relation between phase difference and path difference
Related Solutions
For right-angled prism, ray-1 is the incident ri and ray-2 is the emergent ray as shown in the figure. Refractive index of the prism is .........
View SolutionA ray of light incident normally on one of the faces of a right-angle isosceles prism is found to be totally reflected as shown in the figure. What is the minimum value of the refractive index of the material of the prism? When the prism is immersed in water, trace the path of the emergent ray for the same incident ray, indicating the values of all the angles (mu_omega=4//3) .
View SolutionThe refractive angle of prism is A. A ray is incident normally on one of the refracting faces of a prism and emerges out. If D be the deviation of the ray then refractive index of the material of the prism is—
View SolutionA ray of light is incident is 60^@ on a prism of refracting angle 30^@ . The emerging ray is at an angle 30^@ with the incident ray. The value of refractive index of the prism is:
View SolutionA ray of light is incident horizontally on the face AB of the.right angled prism as shown in the figure. If the ray emerges grazing the surface AC, find the value of . Refractive index of the material of the prism is given to be n.
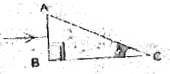
View SolutionFor a ray of light refracted through a prism of angle , the angle of incidence is equal to the angle of emergence, each equal to . Find the refractive index of the material of the prism.
View SolutionFor a ray of light refracted through a prism of angle 60^(@) , the angle of incidence is equal to the angle of emergence, each equal to 45^(@) . Find the refractive index of the material of the prism.
View SolutionAs shown in Fig. is a ray incident on prism . Show the corresponding refracted and emergent rays. The critical angle for the material of the prism is . What is refractive index of the material of prism ?
 .
.
View SolutionThe refracting angle of a prism is 60^(@) and the refractive index of its material is sqrt((7)/(3)). Find the minimum angle of incidence of a ray of light falling on one refracting face of the prism such that the emerging ray will graze the other refracting face.
View SolutionA ray of light is incident at an angle of on one face of a prism . The emergent ray from the prism makes an angle of with the incident ray. The angle of emergence and refractive index of the material of the prism are-
View Solution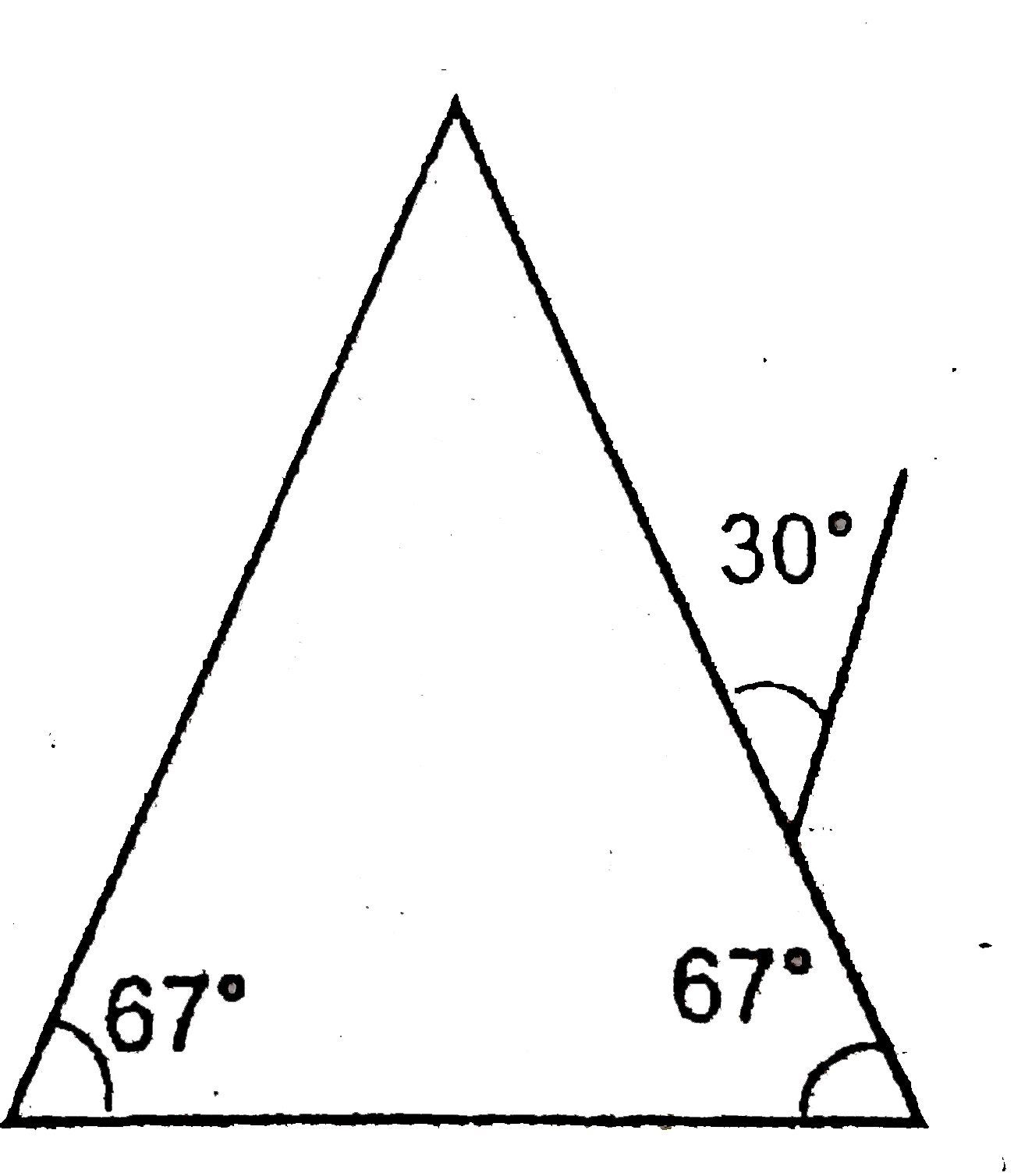
A ray of light incident on one of the face of a prism as shown. After refraction through this surface ray is incident on base of the prism. The refractive index of the prism is . The net deviation of the ray due to prism is
View SolutionA ray of light incident on one of the face of a prism as shown. After refraction through this surface ray is incident on base of the prism. The refractive index of the prism is sqrt(3) . The net deviation of the ray due to prism is
View SolutionA ray PQ incident on face AB of a prism ABC , as shown in Fig., emerges from the face AC such that AQ = AR . Draw the ray diagram showing the pasage of the ray through the prism. If the angle of prism is 60^@ and refractive index of the material of the prism is sqrt(3) , determine the values of angle of incidence and angle of deviation. .
View SolutionWhat is the refractive index of the material of the glass prism shown in the figure, if a ray of light incident normally at the face AB emerges along the face AC?
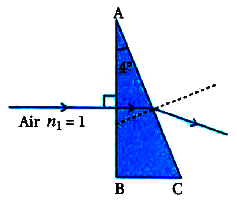
View SolutionA horizontal ray is incident on a right-angled prism with prism angle of 4o. If the refractive index of material of the prism is 1.5, angle of emergence is .......... . Use the given figure.
View SolutionA ray of light falls on a glass prism at a angle of incidence of 30^(@) . Find the direction of the emergent ray if the angle of the prism is 60^(@) and refractive index is 1.50
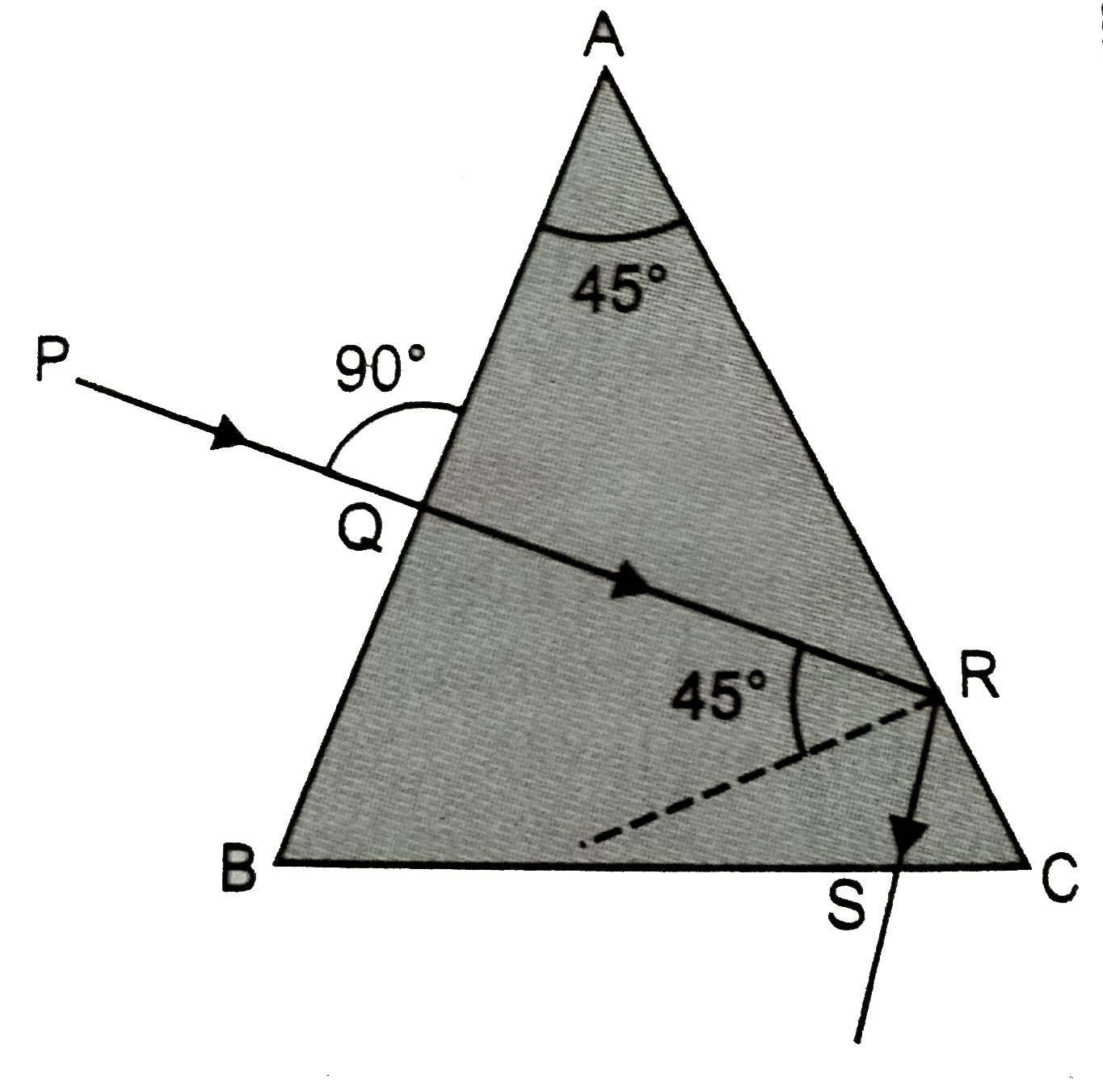
View SolutionA ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism and the refractive index of the material of prism is 3^1/2, then the angle of deviation of the ray is

View SolutionTwo light rays 1 and 2 are incident on two faces AB and AC on an isosceles prism as shown in the figure. The rays emerge from the side BC. Then,

View SolutionAn isosceles prism has one of the refracting surfaces silvered. A ray of light is incident normally on the refracting face AB. After two reflections, the ray emerges from the base of the prism perpendicular to it. Find the angle of the prism.
View SolutionAn isosceles prism has one of the refracting surfaces silvered. A ray of light is incident normally on the refracting face AB. After two reflections, the ray emerges from the base of the prism perpendicular to it. Find the angle of the prism.
View Solution