Question

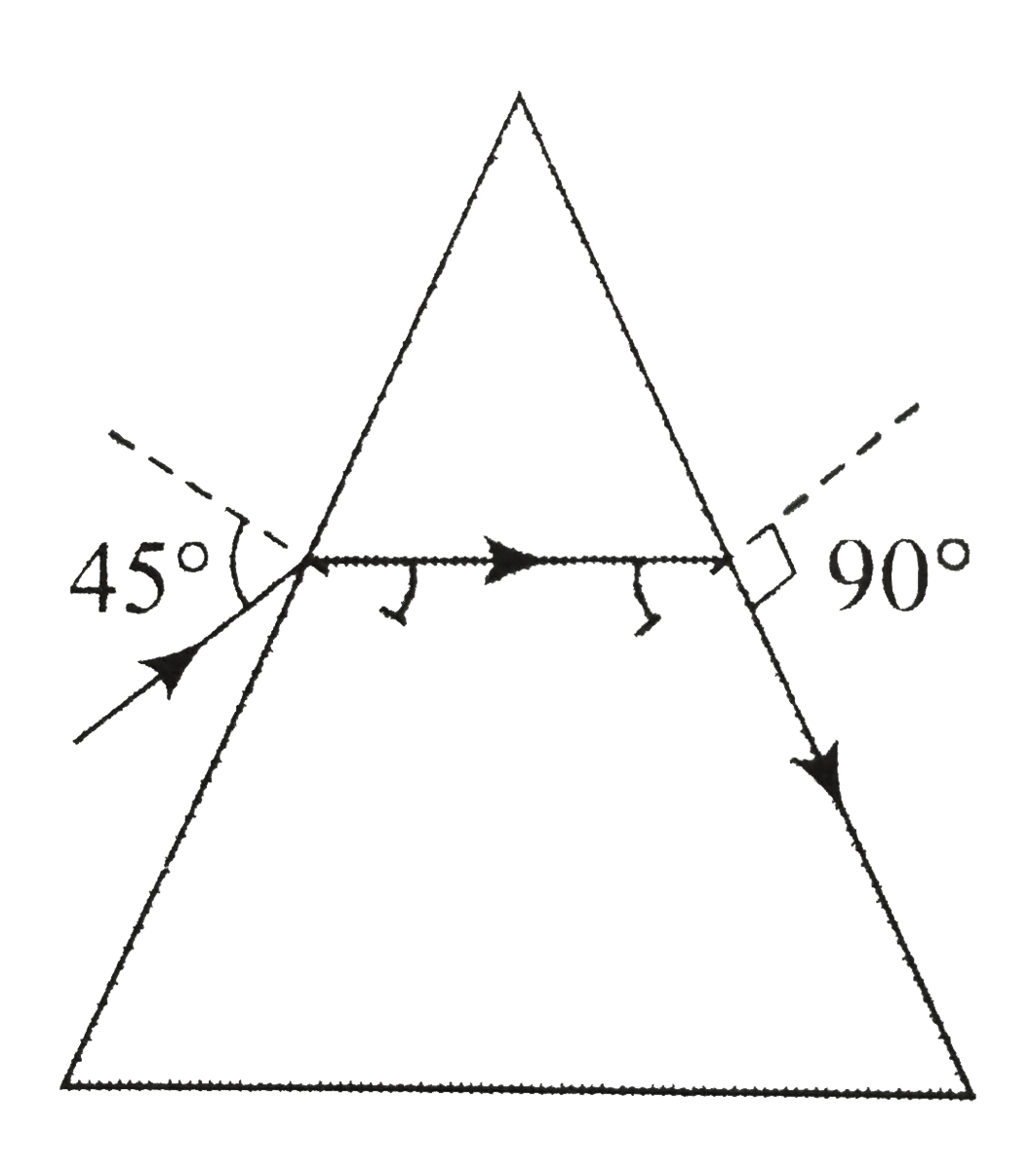
For a ray of light refracted through a prism of angle ${60}^{\circ }$, the angle of incidence is equal to the angle of emergence, each equal to ${45}^{\circ }$. Find the refractive index of the material of the prism.

Answer

1.414

Explanation

To find the refractive index of the material of a prism with an angle of 60 degrees, given that the angle of incidence and the angle of emergence are both 45 degrees, we can follow these steps:

1. Understanding the Geometry of the Prism:
- We have a prism with an apex angle \( A = 60^\circ \).
- The angle of incidence \( i = 45^\circ \) and the angle of emergence \( e = 45^\circ \).

2. Applying Snell's Law at Point A (Incident Ray):
- According to Snell's Law:
\( n_1 \sin(i) = n_2 \sin(R_1) \)
- Here, \( n_1 = 1 \) (refractive index of air), \( i = 45^\circ \), and \( n_2 = n \) (refractive index of the prism).
- Thus, we can write:
\( 1 \cdot \sin(45^\circ) = n \cdot \sin(R_1) \)
- Since \( \sin(45^\circ) = \frac{1}{\sqrt{2}} \):
\( \frac{1}{\sqrt{2}} = n \cdot \sin(R_1) \)
- Rearranging gives:
\( \sin(R_1) = \frac{1}{\sqrt{2} n} \quad \text{(Equation 1)} \)

3. Applying Snell's Law at Point B (Emergent Ray):
- Again using Snell's Law:
\( n \sin(R_2) = n_1 \sin(e) \)
- Here, \( e = 45^\circ \):
\( n \cdot \sin(R_2) = 1 \cdot \sin(45^\circ) \)
- This simplifies to:
\( n \cdot \sin(R_2) = \frac{1}{\sqrt{2}} \)
- Rearranging gives:
\( \sin(R_2) = \frac{1}{\sqrt{2} n} \quad \text{(Equation 2)} \)

4. Relating Angles R1 and R2:
- The sum of the angles \( R_1 \) and \( R_2 \) is equal to the angle of the prism:
\( R_1 + R_2 = A = 60^\circ \)
- Therefore, we can express \( R_2 \) in terms of \( R_1 \):
\( R_2 = 60^\circ - R_1 \)

5. Using the Relationship of Sines:
- From Equations 1 and 2, we have:
\( \sin(R_1) = \sin(60^\circ - R_1) \)
- Since \( R_1 \) and \( R_2 \) are both less than \( 90^\circ \), we can equate:
\( R_1 = R_2 \)
- Thus, \( 2R_1 = 60^\circ \) leading to:
\( R_1 = 30^\circ \)
- Consequently, \( R_2 = 30^\circ \).

6. Finding the Refractive Index:
- Substitute \( R_1 = 30^\circ \) back into Equation 1:
\( \sin(30^\circ) = \frac{1}{\sqrt{2} n} \)
- Since \( \sin(30^\circ) = \frac{1}{2} \):
\( \frac{1}{2} = \frac{1}{\sqrt{2} n} \)
- Rearranging gives:
\( n = \frac{1}{\sqrt{2} \cdot \frac{1}{2}} = \frac{2}{\sqrt{2}} = \sqrt{2} \)
- Therefore, the refractive index \( n \) is:
\( n \approx 1.414 \)

Final Answer:
The refractive index of the material of the prism is approximately \( 1.414 \).