Two equal masses are connected by means of a spring and two other identical springs fixed to rigid supports on either side Fig. 1.3 permit the masses to jointly undergo simple harmonic motion along a straight line so that the system corresponds to two coupled oscillations. Assume that m1 = m2 = m and the stiffness constant is k for both the oscillators. a Form the differential equations for both the oscillators and solve the coupled equations and obtain the frequencies of oscillations. b Discuss the modes of oscillation and sketch the modes.
a Let the mass 1 be displaced by x1 and mass m2 by x2. The force due to the spring on the left acting on mass 1 is −kx1 and that due to the coupling is −kx1 − x2. The net force F1 = −kx1 − kx1 − x2 = −k2x1 − x2 The equation of motion for mass 1 is mx1 + k2x1 − x2 = 0 1 Similarly for mass 2 the spring on the right exerts a force −kx2 and the coupling spring exerts a force −kx2 − x1. The net force F2 = −kx2 − kx2 − x1 = −k2x2 − x1In order that the above equations may have a non-trivial solution the determinant formed from the coefficients of x1 and x2 must vanish.In 12 and 13 the amplitudes are not all independent as we can verify with the use of 7 and 8. Substituting 10 and 12 in 7 yields A2 = A1. Substitution of 11 and 13 in 7 gives B2 = −B1. Dropping off the subscripts on A s and B s the solutions can be written asIf initially x1 = x2 the masses oscillate in phase with frequency ω1 symmetrical mode as in Fig. 1.16a. If initially x2 = −x2 then the masses oscillate out of phase asymmetrical as in Fig. 1.16b
Related Solutions
Two masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
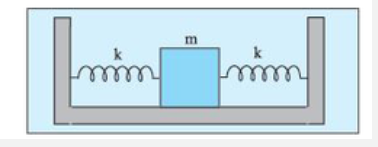
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View SolutionTwo identical springs each of force constant k are connected in parallel and they support a mass mu . Calculate the ratio of the frequency of oscillation of the mass in two systems.
View SolutionTwo identical springs each of force constant k are connected in parallel and they support a mass mu . Calculate the ratio of the frequency of oscillation of the mass in two systems.
View SolutionTwo identical springs each of force constant k are connected in series Calculate the frequency of the system
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
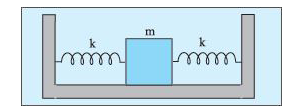
View SolutionTwo springs are connected to a block of mass M is placed on a frictionless surface as shown in figure. If both springs have a spring constant k, the frequency of oscillation of the block is………

View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
View Solutionस्प्रिंग नियतांक k की दो समरूप स्प्रिंगों को चित्र में दर्शाए गए अनुसार m द्रव्यमान एवं स्थिर आधार के एक गुटके से जोड़ा जाता है। दोलनों का आवर्तकाल बताइए।

View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the spring are fixed to firm supports. If each spring has force constant k, the period of oscillation of the body (assuming the spring are massless) is
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K, the period of oscillation of the body (assuming the springs as massless) is :
View Solution