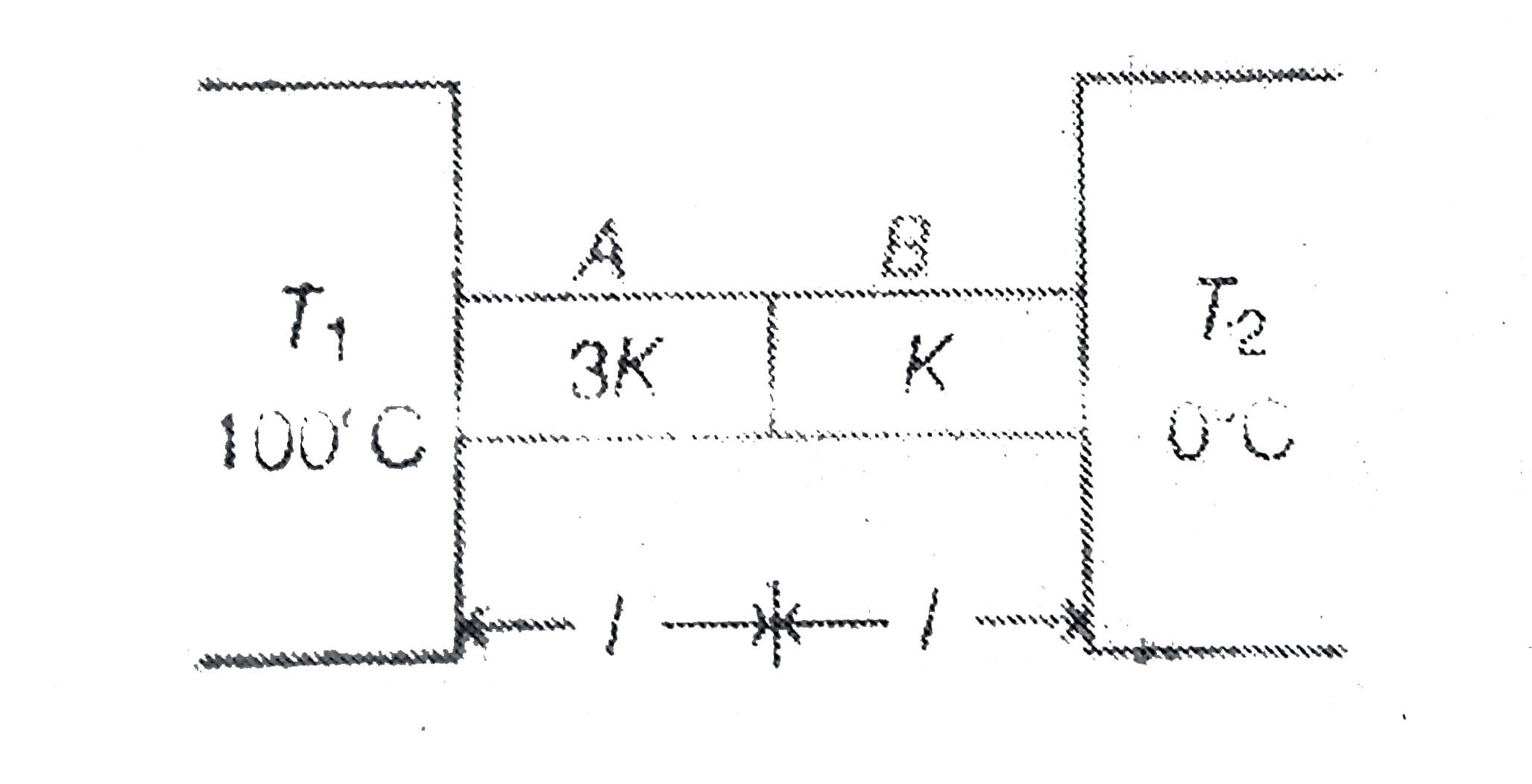
Two rods A and B of same cross-sectional area A and length / connected in series between a source T1 =100°C and a sink T2 = 0°C as shown in figure. The rod is laterally insulated The ratio of the thermal resistance of the rod is
Correct option AExplanation:
Related Solutions
Two rods A and B of same cross-sectional area A and length l are connected in series between a source and a sink as shown in figure. The rod is laterally insulated.
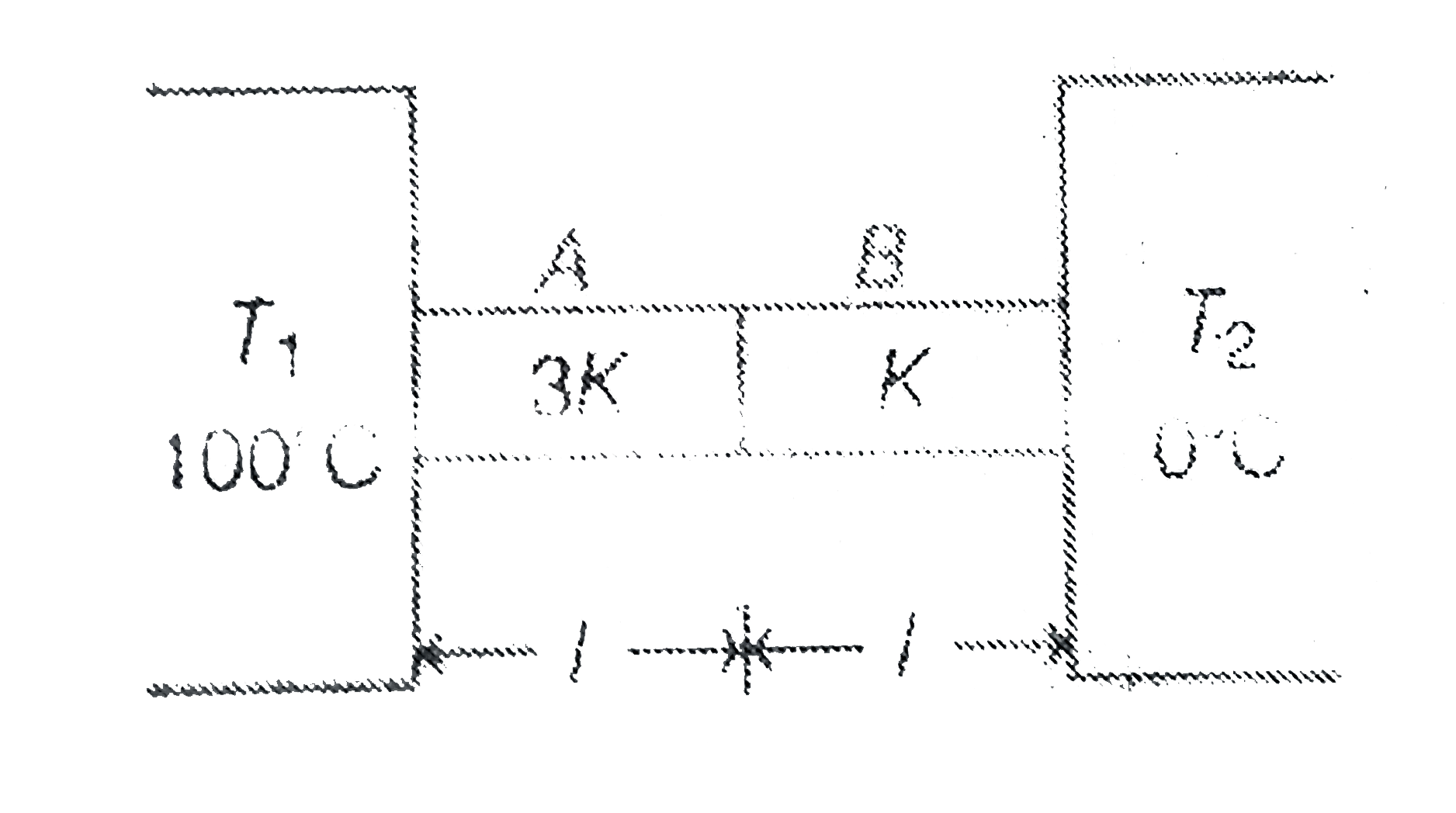
The ratio of the thermal resistance of the rods is
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source and a sink as shown in figure. The rod is laterally insulated.
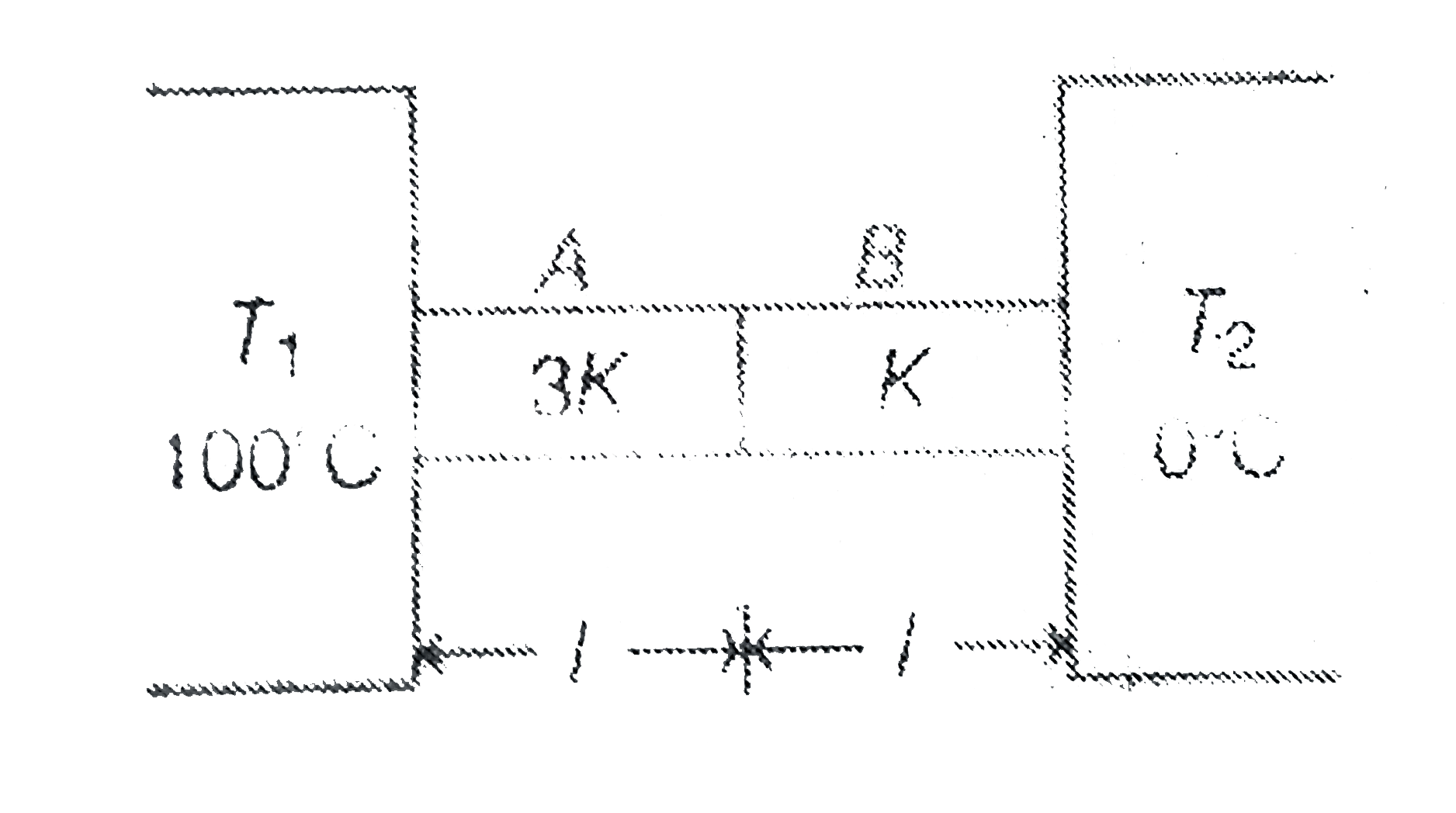
The ratio of the thermal resistance of the rods is
View SolutionTwo rods A and B of same cross-sectional area A and length I are connected in series between a source (T_(1) = 100^(@)C)" and a sink "(T_(2) = 0^(@)C) as shown in figure. The rod is laterally insulated The ratio of the thermal resistance of the rods is
View SolutionTwo rods A and B of same cross sectional are A and length l connected in series between a source (T_(1) =100^(@)C) and a sink (T_(2) =0^(@)C) as shown in The rod is laterally insulated The ratio of thermal resistance of the rod is .
View SolutionTwo rods A and B of same cross-sectional area A and length I are connected in series between a source as shown in figure. The rod is laterally insulated
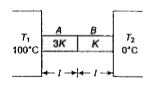
If are the temperature gradients across the rod A and B, then
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source and a sink as shown in figure. The rod is laterally insulated.
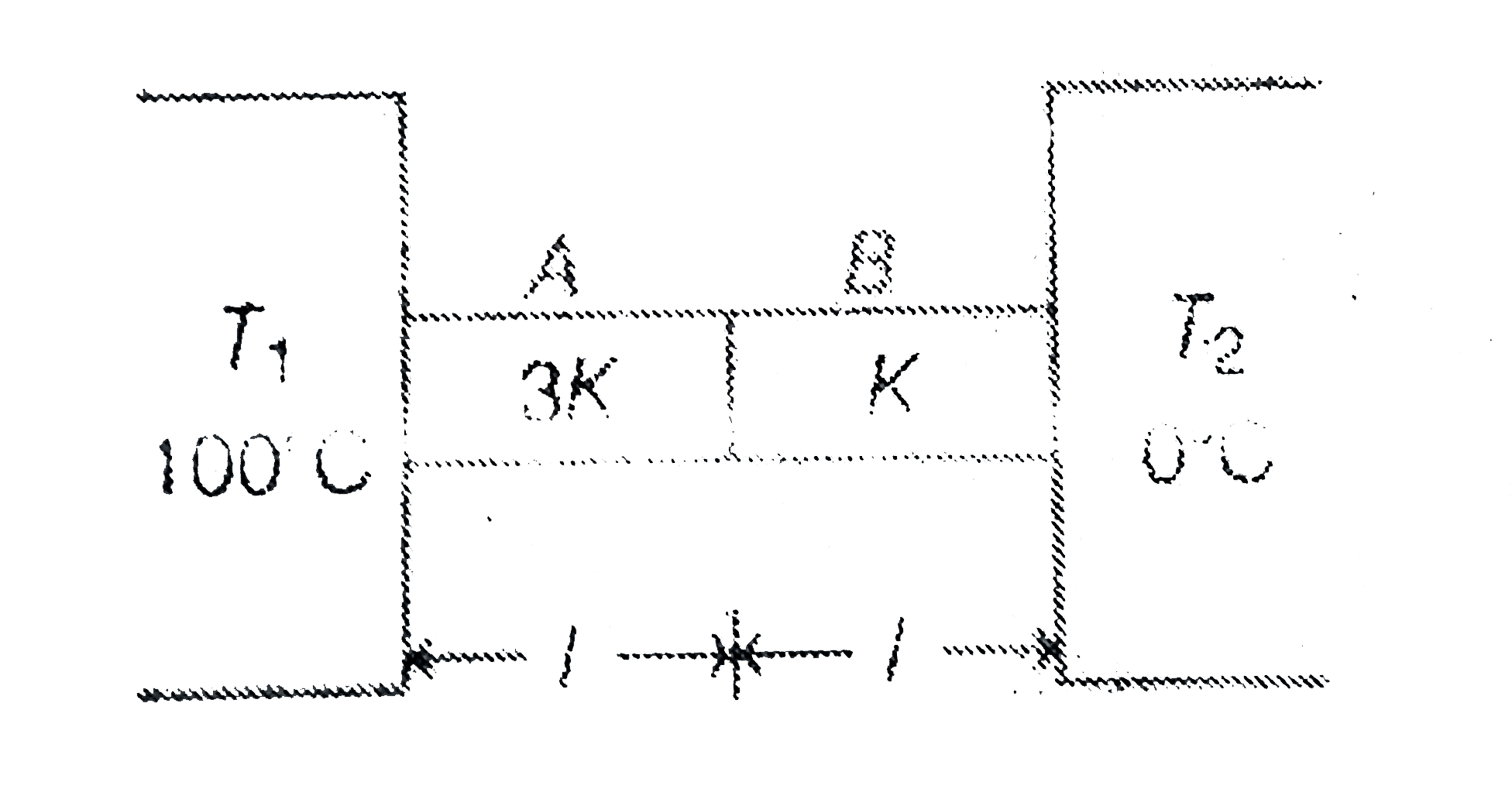
If and are the temperature drops across the rod A and B, then
View SolutionTwo rods A and B of same cross-sectional area A and length I are connected in series between a source (T_(1) = 100^(@)C)" and a sink "(T_(2) = 0^(@)C) as shown in figure. The rod is laterally insulated If T_(A) and T_(B) are the temperature drops across the rod A and B, then
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T_(1)=100^(@)C) and a sink (T_(2)-0^(@)C) as shown in figure. The rod is laterally insulated. If G_(A) and G_(B) are the temperature gradients across the rod A and B, then
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T_(1)=100^(@)C) and a sink (T_(2)-0^(@)C) as shown in figure. The rod is laterally insulated. If T_(A) and T_(B) are the temperature drops across the rod A and B, then
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source and a sink as shown in figure. The rod is laterally insulated.
If and are the temperature gradients across the rod A and B, then
View SolutionTwo rods A and B of same cross sectional are A and length l connected in series between a source (T_(1) =100^(@)C) and a sink (T_(2) =0^(@)C) as shown in The rod is laterally insulated If A_(A) and T_(B) are the temperature drops across temperature gradients the rod A and B then .
View SolutionTwo rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature of the interface will be -
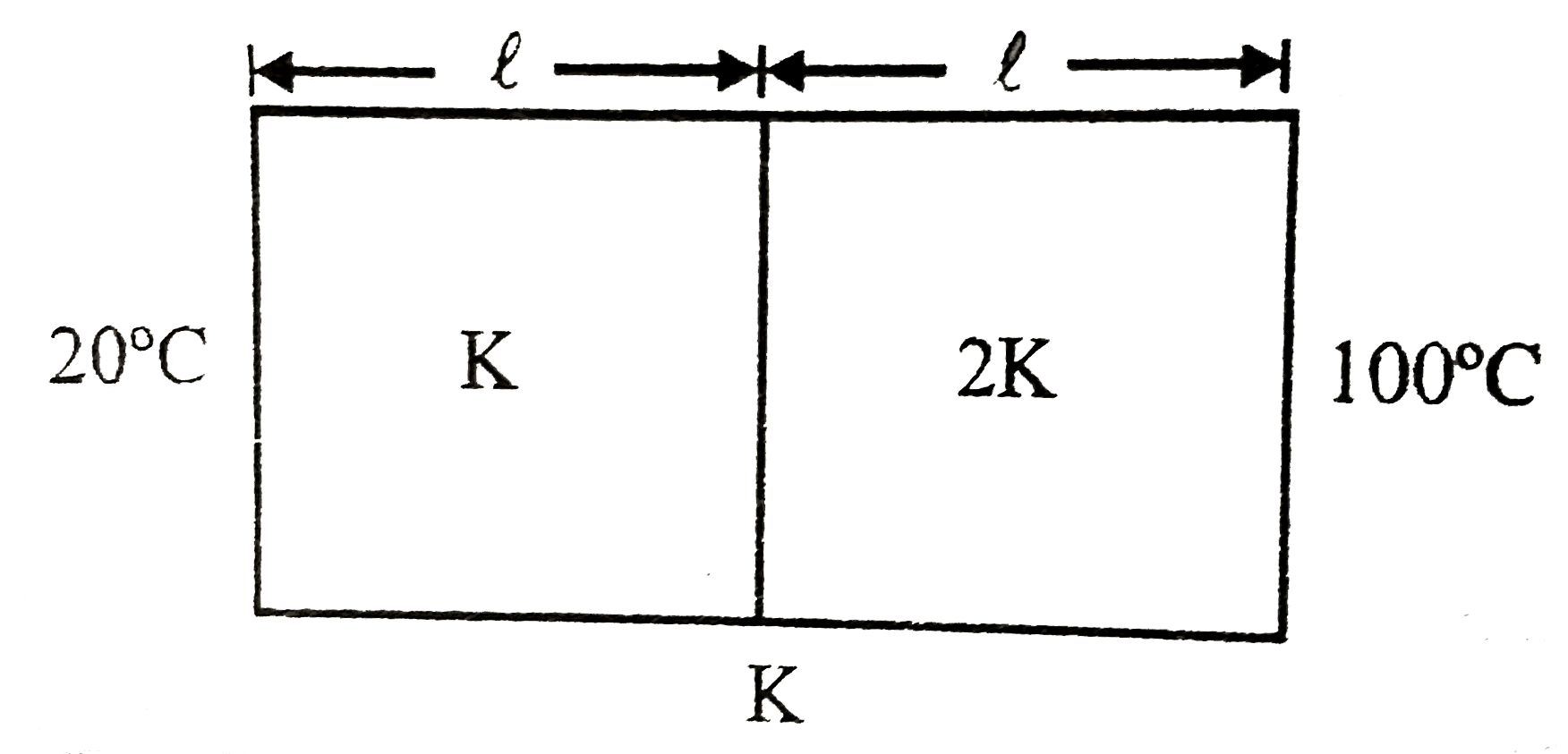
View SolutionThree rods A, B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B , in equilibriu, is
View SolutionThe ratio of thermal conductivity of two rods of different material is . The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionThe ratio of thermal conductivity of two rods of different material is . The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionThe ratio of thermal conductivities of two rods of different material is 5 : 4. The two rods have same area of cross-section and same thermal resistance. They will have the lengths in the ratio
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionThree rods of same length and area of cross-section but of thermal conductivities K, 2K and 3K are connected in series in the same order. Free end of the first rod is at and free end of third rod is at . In steady state, temperature difference across the middle rod is
View SolutionThe ratio of thermal consuctivities of two rods is 5:3 . If the thermal resistances of the two rods of same lengths of the rod is :
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View Solution