The ratio of thermal conductivities of two rods is 5:3. If the thermal resistances of the two rods of same, lengths of the rod is : Solution in Kannada
53
35
23
94
The correct Answer is:A
Thermal resistance R=lkA
Here R1=R2 ⇒ l1k1A1=l2k1A2.
As thickness is same A1=A2.
∴l1l2=k1k2=5/3
Thus correct choice is (a).
Topper's Solved these Questions
- TRANSFERENCE OF HEAT Book:MODERN PUBLICATIONChapter:TRANSFERENCE OF HEAT Exercise:Multiple Choice Questions (Level - III) Questions From AIEEE/JEE Examination)
Explore 5 Videos
- TRANSFERENCE OF HEAT Book:MODERN PUBLICATIONChapter:TRANSFERENCE OF HEAT Exercise:Recent Competitive Questions
Explore 4 Videos
- TRANSFERENCE OF HEAT Book:MODERN PUBLICATIONChapter:TRANSFERENCE OF HEAT Exercise:Recent Competitive Questions
Explore 4 Videos
- SOLIDS & SEMICONDUCTOR DEVICESBook:MODERN PUBLICATIONChapter:SOLIDS & SEMICONDUCTOR DEVICESExercise:Revision Test
Explore 28 Videos
- UNIFORM CIRCULAR MOTIONBook:MODERN PUBLICATIONChapter:UNIFORM CIRCULAR MOTIONExercise:Revision Test
Explore 57 Videos
Similar Questions
A composite block is made of slabs A,B,C,D and E of different thermal conductivities (given in terms of a constant K) and sizes (given in terms of length, L) as shown in the figure. All slabs are of same width. Heat 'Q' flows only from left to right through the blocks.
Then in steady state
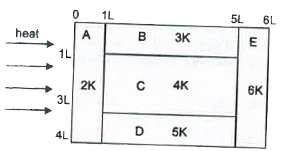
View SolutionTwo slabs are of the thicknesses d1 and d2. Their thermal conductivities are K1 and K2 respectively They are in series. The free ends of the combination of these two slabs are kept at temperatures θ1 and θ2. Assume θ1>θ2. The temperature θ of their common junction is
View SolutionTwo slabs are of the thicknesses d1 and d2. Their thermal conductivities are K1 and K2 respectively They are in series. The free ends of the combination of these two slabs are kept at temperatures θ1 and θ2. Assume θ1>θ2. The temperature θ of their common junction is
View SolutionChoose the forward biased p-n junction :
View SolutionA sphere of mass m is tied to end of a string of length 1 and rotated through the other and along a horizontal circular path with speed . The work done in full horizontal circle is:
View SolutionAssertion : If thermal conductivity of a rod is 5 , then its thermal resistively is 0.2 Reason : Thermal conductivity = (1)/("thermal resistivity")
View SolutionA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionThe ratio of the coefficient of thermal conductivity of two different materials is 5:3. If the thermal resistance of the rod of same thickness resistance of the rods of same thickness of these materials is same, then the ratio of the length of these rods will be
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionTwo rods of equal length and diameter but of thermal conductivities 2 and 3 unites respectively are joined in parallel. The thermal conductivity of the combination is:
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionRatio of thermal conductivities of two different materials is 4:3 To have same thermal resistance of the two rods of having equal thickness, what should be the ratio of their lengths ?
View SolutionThe ratio of the thermal conductivity of two rods is 5: 4 and the area of their transverse-cuts is 1: 1. If the thermal resistance of both rods is the same, then what will be the ratio of lengths of both rods?
View SolutionThe ratio of thermal conductivities of two rods of different material is 5 : 4. The two rods have same area of cross-section and same thermal resistance. They will have the lengths in the ratio
View Solution

