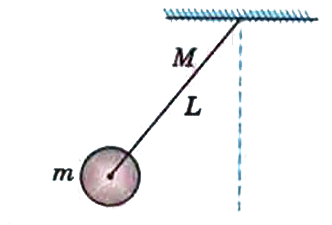
A metal rod of length L and mass m is pivoted at one end. A thin disk of mass M and radius R Angular frequency for case BD Angular frequency for case A< angular frequency for case B
The correct Answer is:Option A
Correct Option A D Explanation: Restoring torque is same in both casesIn case A the moment of inertia is more as compared to B so ωB > ωA
Related Solutions
A dog of mass m is walking on a pivoted disc of radius R and mass M in a circle of radius R//2 with an angular frequency n: the disc will revolve in opposite direction with frequency -
View SolutionA thin uniform vertical rod of mass m and length l pivoted at point O is shown in Fig. The combined stiffness of the springs is equal to k . The mass of the springs is negligible. The angular frequency of small oscillation is
View SolutionA metal rod of length 'L' and maws 'm' is pivoted at one end A thin disc of mass 'M' and radius 'R' ( Which of the folowing statement (s) is (are) true ?
View SolutionOne end of a metal rod of length L and mass M is pivoted to a fixed support and to its free end, a thin disc of mass m and radius r (L) is attached at its centre. In one case, the disc is attached to the rod in such a way that it is not free to rotate about its centre and in another case, teh disc is free to rotate about its centre. When the rod-disc system is displaced slightly from its equilibrium position and released. it peforms S.H.M. in vertical plane. Compare the restoring torque acting on the system and angular frequency in both the cases.
View SolutionLet a thin uniform rod have mass M and length L. In the first case, the axis of rotation passes through the center and is perpendicular to the length of the rod. In the second case, the axis of rotation passes through one end and is perpendicular to the length of the rod. The ratio of the radius of rotation in the first case and the radius of rotation in the second case is:
View SolutionA metal rod of length L and mass m is pivoted at one end. A thin disk of mass M and radius R (lt L) is attached at its center to the free end of the rod. Consider two ways the disc is attached : (case A). The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its centre. The rod disc system perform SHM in vertical plane after being released from the same displaced position. Which of the following statement(s) is (are) true
View SolutionLet 'M' be the mass and 'L' be the length of a thin uniform rod. In first case, axis of rotation is passing through centre and perpendicular to the length of the rod In second case axis of rotation is passing through one end and perpendicular to the length of the rod. The ratio of radius of gyration in first case to second case is
View SolutionLet M be the mass and L be the length of a thin uniform rod. In first case, axis of rotation is passing through centre and perpendicular to the length of the rod. In second case, axis of rotation is passing through one end and perpendicular to the length of the rod. The ratio of radius of gyration in first case to second case is
View SolutionLet M be the mass and L be the length of a thin uniform rod. In first case, axis of rotation is passing through centre and perpendicular to the length of the rod. In second case, axis of rotation is passing through one end and perpendicular to the length of the rod. The ratio of radius of gyration in first case to second case is
View SolutionA uniform chain of mass M and length L is rotated in a horizontal circle about its one end at an angular frequency . The tension at its axis is
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is omega . The force applied on the rod by the pivot is
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is omega . The force applied on the rod by the pivot is
View Solutionk बल नियतांक वाले स्प्रिंग से जुड़े m द्रव्यमान के पिंड की स्वाभाविक कोणीय आवृति होती है -
View SolutionThe angular frequency of a pendulum is rad . If the length is made one fourth of the original length, the angular frequency becomes :
View SolutionA metal rod of length 'L' and mass 'm' is piovted at one end. A thin disk of mass 'M' and radius 'R' (lt L) . Is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A ). The disc is not free to rotate about its centre and (case B ) the disc is free to rotate about its center. The rod-disc sustem perform SHM in vertical plane after being released from the same displaced potion. Which of the following statement(s) is (are) true?
View SolutionA metal rod of length 'L' and mass 'm' is piovted at one end. A thin disk of mass 'M' and radius 'R' (lt L) . Is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A ). The disc is not free to rotate about its centre and (case B ) the disc is free to rotate about its center. The rod-disc sustem perform SHM in vertical plane after being released from the same displaced potion. Which of the following statement(s) is (are) true?
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O . A horizontal force acts at the bottom of the rod. a. Find the angular velocity of the rod as the function of angle of rotation theta. b.What is the maximum angular displacement of the rod?
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O . A horizontal force acts at the bottom of the rod. a. Find the angular velocity of the rod as the function of angle of rotation theta. b.What is the maximum angular displacement of the rod?
View Solutionद्रव्यमान M तथा त्रिज्या R की एक डिस्क चित्रानुसार कोणी चाल से क्षैतिज तल पर लुढृक रही है। मूलबिंदु O के परितः डिस्क के कोणीय संवेग का परिमाण है
View SolutionA uniform rod mass m and length l is provided at one end and is rotated with constant angular velocity omega in a horizontal plane. Tension in the rod at a distance (√3l/2) from pivoted end is (Assume gravity free space)
View Solution