A ray of light travelling in air is incident at angle of incident 300 on one surface of slab in which refractive index varies with y. The light travels along the curve y=4 x2 y & x are in meter in the slab. Find out the refractive index of the slab at y=1/2m in the slab a μ =3/2 b 4/3 c 9/8 d none
Correct option is a μ=3/2.Explanation:Let R.I at y=y1 is μ and corresponding angle of refraction is θ μ sin θ=1.sin 30 tan [π/2-θ] = dy/dx = cot θ y=4x2 dy/dx = d/dx4x2 = 8x = cot θ cot θ = 8x = 8y/a1/2 =4y1/2 cot θ = 4y1/2 at y=1/2 cot θ = 4/√2 =2√2 sin θ=1/3 μ sin θ =1 sin 30 μ 1/3 =1/2 μ=3/2
Related Solutions
A ray of light travelling in air is incident at angle of incidence on one surface of a slab in which refractive index varies with y. The light travels along the curve (y and x are in meter) in the slab. Find out the refractive index of the slab at y = 1/2 m in the slab.
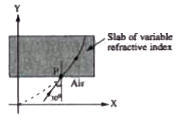
View SolutionA ray of light travelling in air is inciden at angle of inciden on one surface of slab in which refractive index varies with y. The light travels along the curve ( y and x are in meter) in the slab. Find out the refractive index of the slab at in the slab.

View SolutionA ray of light travelling in air is inciden at angle of inciden 30^@ on one surface of slab in which refractive index varies with y. The light travels along the curve y =4x^(2) ( y and x are in meter) in the slab. Find out the refractive index of the slab at y=1//2m in the slab.
View SolutionA ray of light in air is incident at angle of incident 30^(@) on one surface of slab in which refractive index varies with y-axis. Light travels along the curve y=4x^(2) in the slab. If refractive index of the slab at y=(1)/(2)m in the slab is (alpha)/(2) find alpha .
View SolutionA ray of light enters a rectangular glass slab of refractive index at an angle of incidence . It travels a distance of 5cm inside the slab and emerges out of the slab. The perpendicular distance between the incident and the emergent rays is
View SolutionA ray of light enters a rectangular glass slab of refractive index at an angle of incidence . It travels a distance of 5cm inside the slab and emerges out of the slab. The perpendicular distance between the incident and the emergent rays is
View SolutionA monochromatic light of wavelength 4800 A travelling in air is incident on a glass slab of refractive index 1.5, its wavelenght in glass slab is
View SolutionA monochromatic light of wavelength 4800 A travelling in air is incident on a glass slab of refractive index 1.5, its wavelenght in glass slab is
View SolutionA ray of light travelling in air falls on the surface of a transparent slab. The ray makes an angle of 45^@ with the normal to the surface. Find the angle made by the refracted ray with the normal within the slab. Refractive index of the material of the slab =sqrt2.
View SolutionA ray of light incident on a slab of transparent material is partly reflected from the surface and partly refracted into the slab. The reflected and refracted rays are mutually perpendicular. The incident ray makes an angle i with the normal to the slab. the refreactive index of the slab is
View SolutionA ray of light is incident at an angle of incidents 60^(@) on a transparent glass slab. The angle between the reflected ray and the refracted ray is 90^(@) . What is the refractive index of the slab?
View SolutionQ."4 A light ray travels in a glass slab of refractive index mu=2 .Find the time taken by the light ray to travel in the glass slab for a distance of 20sqrt(3)d (Velocity of light =c )
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by . If the thickness of the slab is , determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by mu=sqrt((1+y) . If the thickness of the slab is d=2m , determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA light ray is incident on a plane glass slab of thickness ‘t’ at an angle of incidence ‘i’ as shown in the figure. If mu is the refractive index of glass. Then find time taken by the light ray to travel through the slab.
View SolutionA light ray is incident on a plane glass slab of thickness t at an angle of incidence t as shown in the figure . If mu is the refractive index of glass. Then find time taken by the light ray to travel through the slab.
View SolutionA ray of light travelling inside a glass slab of refractive index is incident on the glass air interface at an angle of incidence of . The refractive index of the air is one. In the case, the ray :
View SolutionA ray of light is incident on a glass slab making an angle of with the surface. The angle of refraction in glass, if the refractive index of flass is 1.6 , is
View SolutionA ray of light is incident on a glass slab of refractive index 1.5 making an angle of with the surface. The angle of refraction in glass is :
View SolutionA ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40^(@) with the surface. The angle of refraction in glass is
View Solution