A ray of light enters a rectangular glass slab of refractive index √3 at an angle of incidence 60∘. It travels a distance of 5cm inside the slab and emerges out of the slab. The perpendicular distance between the incident and the emergent rays is
5√3cm
52cm
5√3/2cm
5cm
The correct Answer is:b.
To solve the problem, we need to determine the perpendicular distance between the incident ray and the emergent ray after the ray of light passes through a rectangular glass slab. Here’s a step-by-step solution:
Step 1: Identify the given values
- Refractive index of the glass slab, n=√3
- Angle of incidence, i=60∘
- Distance traveled inside the slab, d=5cm
Step 2: Apply Snell's Law at the air-glass interface
Using Snell's Law:
n1sin(i)=n2sin(r)
where n1=1 (for air), n2=√3, i=60∘, and r is the angle of refraction in the glass.
Substituting the values:
1⋅sin(60∘)=√3⋅sin(r)
sin(60∘)=√32
So,
√32=√3⋅sin(r)
Dividing both sides by √3:
sin(r)=12
Thus, r=30∘.
Step 3: Calculate the angle of emergence
When the ray exits the slab, it will again follow Snell's Law. The angle of incidence at the second interface (glass-air) will be equal to the angle of refraction r we just calculated, which is 30∘.
Using Snell's Law again:
√3⋅sin(30∘)=1⋅sin(e)
Since sin(30∘)=12:
√3⋅12=sin(e)
sin(e)=√32
Thus, e=60∘.
Step 4: Determine the perpendicular distance
The total angle of deviation from the normal as the ray enters and exits the slab is:
Total deviation=i+e−180∘=60∘+60∘−180∘=−60∘
However, we are interested in the perpendicular distance d between the incident and emergent rays.
Using the geometry of the situation, we can relate the perpendicular distance D to the angles:
D=d⋅sin(i−r)
Substituting d=5cm, i=60∘, and r=30∘:
D=5⋅sin(60∘−30∘)
D=5⋅sin(30∘)
D=5⋅12=2.5cm
Final Answer
The perpendicular distance between the incident and emergent rays is 2.5cm.
---
- Refractive index of the glass slab, n=√3
- Angle of incidence, i=60∘
- Distance traveled inside the slab, d=5cm
Using Snell's Law:
n1sin(i)=n2sin(r)
where n1=1 (for air), n2=√3, i=60∘, and r is the angle of refraction in the glass.
1⋅sin(60∘)=√3⋅sin(r)
sin(60∘)=√32
So,
√32=√3⋅sin(r)
Dividing both sides by √3:
sin(r)=12
Thus, r=30∘.
When the ray exits the slab, it will again follow Snell's Law. The angle of incidence at the second interface (glass-air) will be equal to the angle of refraction r we just calculated, which is 30∘.
√3⋅sin(30∘)=1⋅sin(e)
Since sin(30∘)=12:
√3⋅12=sin(e)
sin(e)=√32
Thus, e=60∘.
The total angle of deviation from the normal as the ray enters and exits the slab is:
Total deviation=i+e−180∘=60∘+60∘−180∘=−60∘
However, we are interested in the perpendicular distance d between the incident and emergent rays.
D=d⋅sin(i−r)
Substituting d=5cm, i=60∘, and r=30∘:
D=5⋅sin(60∘−30∘)
D=5⋅sin(30∘)
D=5⋅12=2.5cm
The perpendicular distance between the incident and emergent rays is 2.5cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
Light enters in a glass slab of refractive index 3/2 and covers a distance 20 cm. The optical path of it is
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View Solution
Knowledge Check
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
A75∘B90∘C105∘D120∘
A ray of light is incident on a rectangular plate at an angle of incidence 60∘. The light ray suffers a deviation which is 25% of the angle of incidence. The refractive index of the glass will be
View SolutionA glass plate has a thicknes t and refractive index μ. The angle of incidence of a ray from air into the plate is equal to the critical angle for glass air intrerface. The lateral shift (perpendicular distance between incident ray and emergent ray) of ray is given by
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light is incident on a transparent glass slab of refractive index √3. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence?
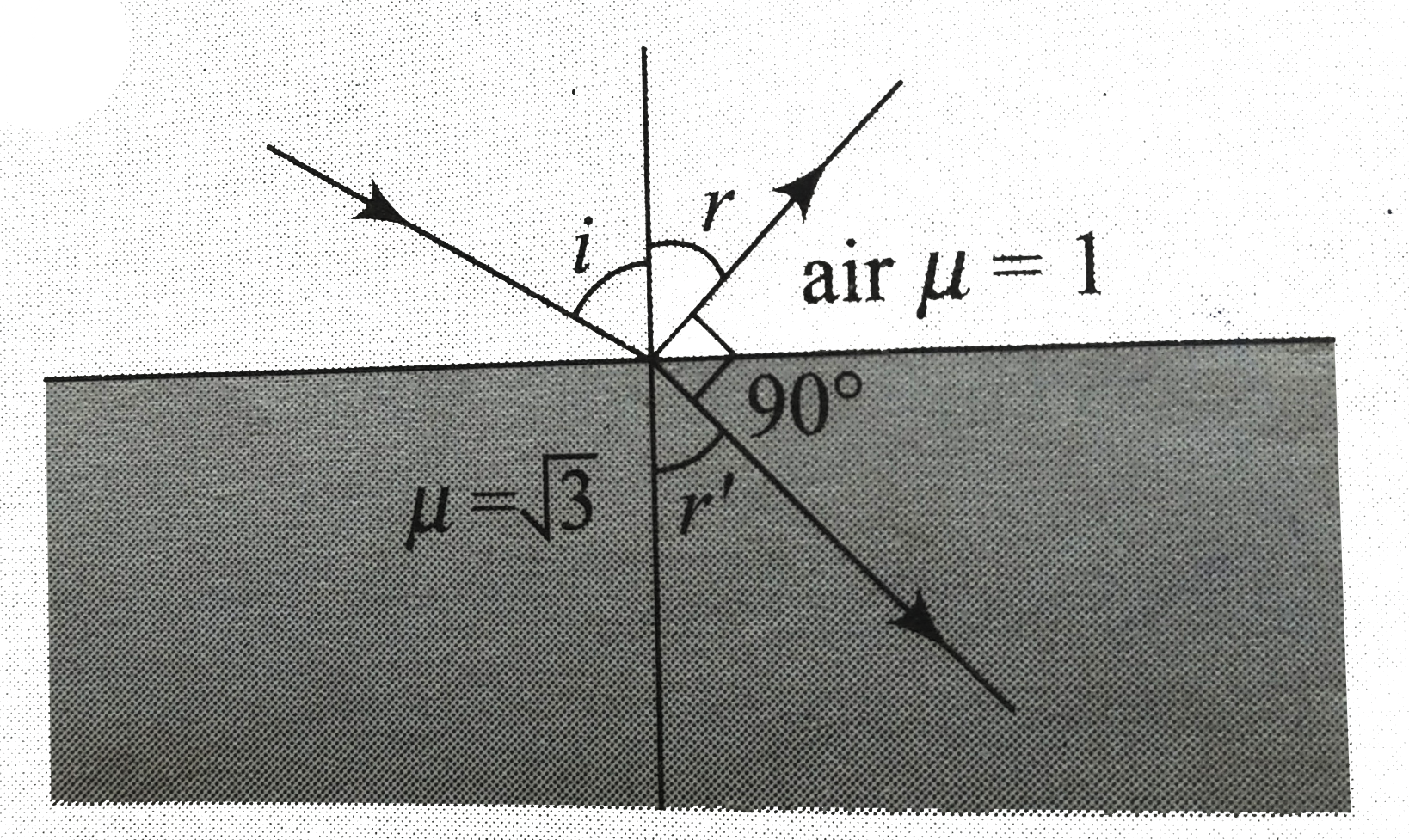
View SolutionA ray of light is incident on one face of a transparent glass slab of thickness 9cm at an angle of incidence 60∘. Lateral displacement of the ray on emerging from the opposite parallel face is 3√3cm. Refractive index of the material of slab is:
View SolutionA ray of light falls normally on a rectangular glass slab.
Draw a ray diagram showing the path of the ray till it emerges out of the slab.
View Solution
