A ray of light travelling in air is incident at grazing angle angle of incidence ≈ 900 on a long rectangular slab of a transparent media of thickness t=1.0m. The point of incidence is the origin A0 0. The medium has a variable refractive index given by ny=ky3/2+11/2 Where k=1.0m-3/2 the refractive index of air is 1 1. Obtain a relation between the slope of the trajectory of the ray at appoint Bx y in the medium and the incidence angle at that point a cot θ = dy/dx b tan θ = dy/dx c cot θ = 1/2dy/dx d none 2. Obtain an equation for the trajectory yx of the ray in the medium a y=K2x/44 b y=kx2 c y=kx/42 d none 3. Determine the coordinatesx1 y1 of the point p where the ray intersects the upper surface of the slap-air boundary a 4m 1m b 2m 1m c 1m 1m d none 4. Indicate the path of the ray subsequently. a The ray will emerge parallel to boundary b Perpendicular to boundary c Neither a nor b d Data insufficient
1 Trajectory of the curve is shown by dotted curve the slope of the target at point B tan ɸ= dy/dx The angle of incidence at B is θ=90-ɸ tan ɸ=tan 90-θ=cot θ= dy/dx2 from Snell’s law at A and B 1 sin 90=ny sinθ 2 sinθ= 1/ny = 1/[ky3/2 +1]1/2 3 cosθ= √1-sin2θ =√1- [1/[ky3/2 +1]1/2] cot θ = cos θ/sin θ =[√1- [1/[ky3/2 +1]1/2]]/[1/[ky3/2 +1]1/2] cot θ = √[ky3/2 +1-1/ ky3/2 +1]/[ 1/[ky3/2 +1]1/2] cot θ= √[ky3/2/ ky3/2 +1][ [ky3/2 +1]1/2] cot θ= k1/2y3/4 ........4 From equation 3 Sinθ =1/ny = cos ɸ= 1/[√1+tan2ϕ] cot θ=cot90-ɸ=tan ɸ 1/ny = 1/[√1+cot2θ] ny= √1+cot2θ = √1 +dy/dx2[ky3/2 +1]1/2 = √1 +dy/dx2 dy/dx2 =ky3/2 dy/dx = k1/2y3/2 ∫[dy/y]3/4 = ∫k1/2dx ∫y-3/4 = √k ∫dx [y-3/4]/[-3/4+1]=√k x +c 4y1/4=√kx +c Applying boundary condition x=0 y=0 c=0 4y1/4=√k x y1/4= √k/4 xy = k2x/443 At point P x=? y=1 k=1 1= k2 x/44 1=1x/44 1=x/4 x=4m The coordinates of P 4 1 4 From Snell’s law nA sin iA=nP sin iP iA=iP=90 The ray will emerge parallel to the boundaries
Related Solutions
A ray of light travelling in air is incident at grazing angle (incident angle = 90^@ ) on a large rectangular slab of a transparent medium of thickness t = 1 m. The point of incidence js the origin A (0, 0). The medium has a refractive index of n (y) given n(y)= (9ky^(3/2)+ 1)^(1/2) Where K = ("meter")^((-3)/2) , The refractive index of air is 1. Obtain the equation for the trajectory y(x) of the ray of the medium.
View SolutionA ray of light travelling in air is incident at grazing angle (incident angle= 90^(@)) on a long rectangular slab of a transparent medium of thickness t=1.0 (see figure). The point of incidence is the origin A(O,O) .The medium has a variable index of refraction n(y) given by : n(y)=[ky^(3//2)+1]^(1//2) ,where k= 1.0m^(-3//2) .the refractive index of air is 1.0 (i) Obtain a relation between the slope of the trajectory of the ray at a point B(x,y) in the medium and the incident angle at that point (ii) obtain an equation for the trajectory y(x) of the ray in the medium. (ii) Determine the coordinates ( x_(1),y_(1)) of the point P .where the ray the ray intersects upper surface of the slab -air boundary. Indicate the path of the ray subsequently.
View SolutionA ray of light travelling in air is incident at grazing angle (incident angle= 90^(@)) on a long rectangular slab of a trasnparent medium of thickness t=1.0 (see figure). The point of incidence is the origin A(O,O) .The medium has a variable index of refraction n(y) given by : n(y)=[ky^(3//2)+1]^(1//2) ,wherek= 1.0m^(-3//2) .the refrative index of air is 1.0 (i) Obtain a relation between the slope of the trajectory of the ray at a point B(x,y) in the medium and the incident angle at that point (ii) obtain an equation for the trajectory y(x) of the ray in the medium. (ii) Determine the coordinates ( x_(1),y_(1)) of the point P .where the ray the ray intersects upper surface of the slab -air boundary. Indicate the path of the ray subsequently.
View SolutionA ray of light travelling in air is incident on the plane surface of a transparent medium. The angle of incidence is and the angle of refraction is . Find the refractive index of the medium .
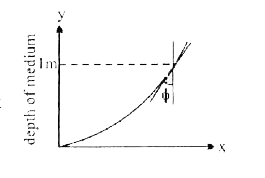
View SolutionA ray of light travelling in air is incident at grazing angle (incidence angle ) on a medium whose refractive index depends on the depth of the medium. The trajectory of the light in the medium is a parabola, . Find, at a depth of 1 m in the medium
(i) the refractive index of the medium and
(ii) angle of incidence .
View SolutionA ray of light travelling in air is incident at 45^(@) on a medium of refractive index sqrt(2) . The angle of refractive in the medium is
View SolutionA ray of light travelling inside a rectangular glass block of refractive index is incident on the glass–air surface at an angle of incidence of . The refractive index of air is 1. Under these conditions the ray
View SolutionA ray of light is incident at an angle of incidents 60^(@) on a transparent glass slab. The angle between the reflected ray and the refracted ray is 90^(@) . What is the refractive index of the slab?
View SolutionA ray of light strikes a transparent rectangular slab of refractive Index sqrt(2) at an angle of incidence of 45^@ . The angle between the reflected and refracted ray is :
View SolutionA ray of light is incident on a medium of refractive index sqrt(2) at an angle of incidence of 45^(@) . The ratio of the width of the incident beam in air to that of the refracted beam in the medium is
View SolutionA ray of light passes from vacuum into a medium of refractive index n . If the angle of incidence is twice the angle of refraction , then the relation between the angle of incidence and the refractive index is
View SolutionA ray of light travelling inside a rectangular glass block of refractive indexis incident on the glass-air surface at an angle of incidence of . The refractive index of air is one. Under these conditions the ray will
View SolutionA ray of light strikes a transparent rectangular slab of refractive index at an angle of incidence of . The angle between the reflected and refracted rays is
View SolutionA ray of light strikes a transparent rectangular slab of refractive index sqrt(2) at an angle of incidence of 45^(@) . The angle betweent the reflected and refracted rays is
View SolutionA ray of light travelling inside a rectangular glass of block of refractive indx is incident on the glass air surface at an angle of incidence of . the refractive index of air is 1 . The ray will
View SolutionA ray of light travelling in air is incident at on a midium of refractive index . The angle of refraction in the medium is :
View SolutionLight traveling from a transparent medium to air undergoes that internal reflection at an angle of incident of . Then refractive index of the medium may be
View Solutiona ray of light sqrt(2) It strikes a transparent slab of refractive index 45° at an angle of incidence. The angle between the reflected and refracted rays is:
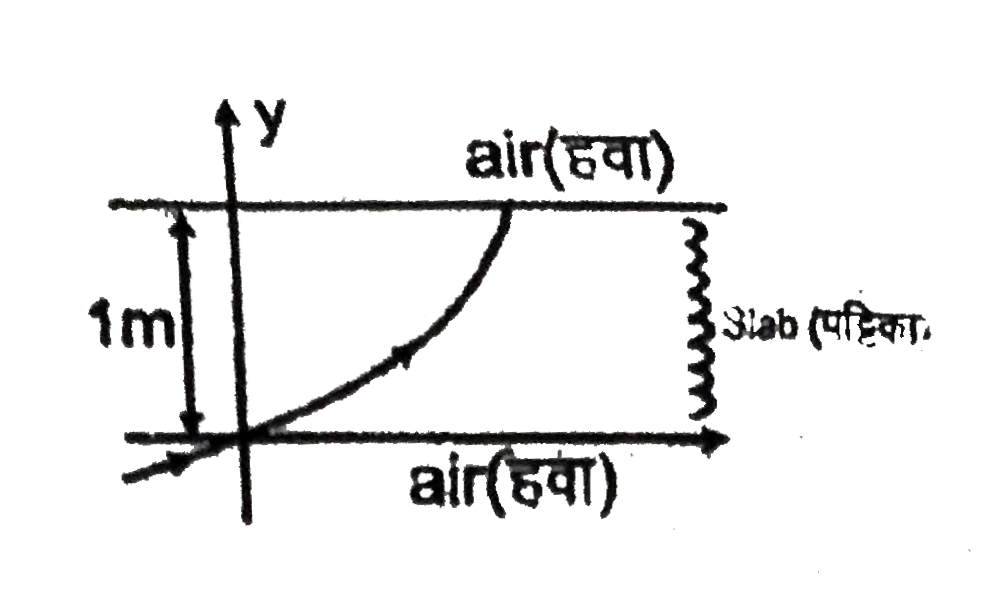
View SolutionA ray of light travelling in air is incident at grazing incidence on a slab with variable refractive index, n where and follows path as shown in the figure. What is the total deviation produced by slab when the ray comes out.
View Solution