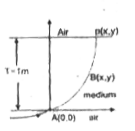
A ray of light travelling in air is incident at grazing angle (incident angle=90∘) on a long rectangular slab of a trasnparent medium of thickness t=1.0(see figure). The point of incidence is the originA(O,O) .The medium has a variable index of refraction n(y) given by :n(y)=[ky3/2+1]1/2,wherek=1.0m−3/2.the refrative index of air is 1.0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_RO_C01_E01_029_Q01.pngwh=80%mx-autosty≤=background:white;><br>(i)Obta∈arelationbetweentheslopeofthetrajec→ryoftherayatap∮B(x,y)∈themediumandthe∈cnt∠attˆp∮<br>(ii)obta∈anequationforthetrajec→ryy(x)oftheray∈themedium.<br>(ii)Determinethec∞rd∈ates(x_(1),y_(1))ofthep∮P.where the ray the ray intersects upper surface of the slab -air boundary.
Indicate the path of the ray subsequently.
The correct Answer is:(i)tanθ=dydt=coti;(ii)1,(iii)y=k2(x/4)4;(iv)4.0,1;(v) it will become parallel to x-axis.

(i)slope =dydx=tanθ⇒dydx=tan(90−i)
dydx=coti……….(1)
(ii) Applying snell's law between point of incidence and at point B.
ny.sini=1×sin90∘
ny.sini=1
(iii)[ky3/2+1]1/21coseci=1⇒[ky3/2+1]1/21√1+cot2i=1
[ky3/2+1]1/2=√(1+cot2)i.....(2)
From (1)&(2)
[ky3/2+1]=1+(dydx)2⇒ky3/2=(dydx)2⇒dydx=√ky3/4
4∫0y−34=√kX∫0dx⇒⎡⎢⎣y−34+1−34+1⎤⎥⎦y0=√k[X]X0⇒4y1/4=√kX
y=k2(x44)
(iv)1=k2(x44)⇒1=(1)2.(x44)
x=4
(iv)Ray will emage parallel to incident ray means parallel to x-axis.
Similar Questions
A ray of light travelling in air is incident at grazing angle (incident angle = 90∘) on a large rectangular slab of a transparent medium of thickness t = 1 m. The point of incidence js the origin A (0, 0). The medium has a refractive index of n (y) given
n(y)=(9ky32+1)12
Where K = (meter)−32, The refractive index of air is 1.
Obtain the equation for the trajectory y(x) of the ray of the medium.
View SolutionA ray of light travelling in air is incident on the plane surface of a transparent medium. The angle of incidence is 45∘ and the angle of refraction is 30∘ . Find the refractive index of the medium .
View Solution
Knowledge Check
A ray of light travelling in air is incident at 45∘ on a medium of refractive index √2. The angle of refractive in the medium is
AA. 45∘BB.60∘CC.30∘DD.70∘A ray of light is incident at an angle of incidence 45∘ on an equilateral prism and emerge at an angle 45∘ then the refractive index of the medium of the prism is:
A2B√2C1√2D√3AN unpolarised beam of light is incident at the polarising angle on the surface of a transparent medium of refractive index 1.6. The angle of refraction in the medium is
A58∘B29∘C32∘D42∘
A ray of light travelling in air is incident at grazing angle (incidence angle =90∘) on a medium whose refractive index depends on the depth of the medium. The trajectory of the light in the medium is a parabola, y=2x2. Find, at a depth of 1 m in the medium
(i) the refractive index of the medium and
(ii) angle of incidence ϕ.
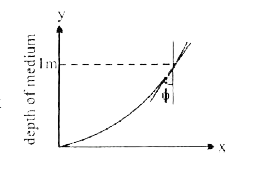
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light is incident at an angle of 60∘ on one face of a rectangular glass slab of thickness 0.1m, and refractive index 1.5.Calculate the lateral shift produced.
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√1+√y. If the thickness of the slab is d, determine the equation ofthe trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light is incident at an angle of 60∘ on one face of a rectangular glass slab of thickness 0.1m, and refractive glass slab of thickness 0.1m, and refractive index 1.5. Calculate the lateral shift produced.
View Solution