A ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√1+√y. If the thickness of the slab is d, determine the equation ofthe trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
To solve the problem step by step, we will analyze the situation of a ray of light incident at grazing incidence on a glass slab and derive the trajectory of the ray inside the slab, as well as the coordinates of the exit point.
Step 1: Understand the Geometry
The ray of light is incident at grazing incidence, which means it strikes the surface of the glass slab at an angle of 90 degrees. The refractive index of the glass slab is given by:
μ=√1+√y
where y is the vertical coordinate.
Step 2: Apply Snell's Law
At the point of incidence, we can apply Snell's law. Since the angle of incidence is 90 degrees, we have:
n1sin(90∘)=n2sin(θ)
Here, n1=1 (for air) and n2=μ. Thus,
1⋅1=μ⋅sin(θ)
This implies:
sin(θ)=1μ
Step 3: Find the Value of cot(θ)
Using the relationship of sine and cotangent, we can express cot(θ):
cot(θ)=cos(θ)sin(θ)=√1−sin2(θ)sin(θ)
Substituting sin(θ)=1μ:
cot(θ)=√1−(1μ)21μ=μ√1−1μ2=μ√μ2−1μ2=√μ2−1
Step 4: Relate the Slope to the Trajectory
The slope of the trajectory at point P can be expressed as:
dydx=cot(θ)
Substituting the expression for cot(θ):
dydx=√μ2−1
Step 5: Substitute the Refractive Index
Substituting μ=√1+√y:
dydx=√(1+√y)−1=√√y=y1/4
Step 6: Separate Variables and Integrate
Now we can separate variables:
dyy1/4=dx
Integrating both sides:
∫y−1/4dy=∫dx
The left side integrates to:
43y3/4=x+C
Step 7: Solve for the Constant of Integration
At the point of entry (origin), when x=0, y=0:
43(0)3/4=0+C⟹C=0
Thus, we have:
43y3/4=x⟹y3/4=34x⟹y=(34x)4/3
Step 8: Find the Exit Point
The thickness of the slab is d. Setting y=d:
d=(34x)4/3
Solving for x:
x=43d3/4
Step 9: Coordinates of Exit Point
The coordinates of the exit point P are:
(x,y)=(43d3/4,d)
Final Answer
The trajectory of the ray inside the slab is given by:
y=(34x)4/3
And the coordinates of the exit point are:
(43d3/4,d)
The ray of light is incident at grazing incidence, which means it strikes the surface of the glass slab at an angle of 90 degrees. The refractive index of the glass slab is given by:
At the point of incidence, we can apply Snell's law. Since the angle of incidence is 90 degrees, we have:
Using the relationship of sine and cotangent, we can express cot(θ):
The slope of the trajectory at point P can be expressed as:
Substituting μ=√1+√y:
Now we can separate variables:
At the point of entry (origin), when x=0, y=0:
The thickness of the slab is d. Setting y=d:
The coordinates of the exit point P are:
The trajectory of the ray inside the slab is given by:
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFLECTION)
9 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFRECTION)
28 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
A ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y). If the thickness of the slab is d, determine the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
[y=x24]
View Solution
Knowledge Check
A ray of light is incident on a glass slab at an angle of 45∘. If refractive index of glass be 1.6, what is the angle of refraction ?
A45.2∘B30∘C26.2∘D15.2∘A ray of light 10−9 second to cross a glass slab of refractive index 1.5. The thickness of the slab will be
A0.1 mB0.2 mC0.3 mD0.4 mA ray of light is incident on a parallel-sided glass slab as shown in the figure. The angle of refraction for this ray of light is likely to be :
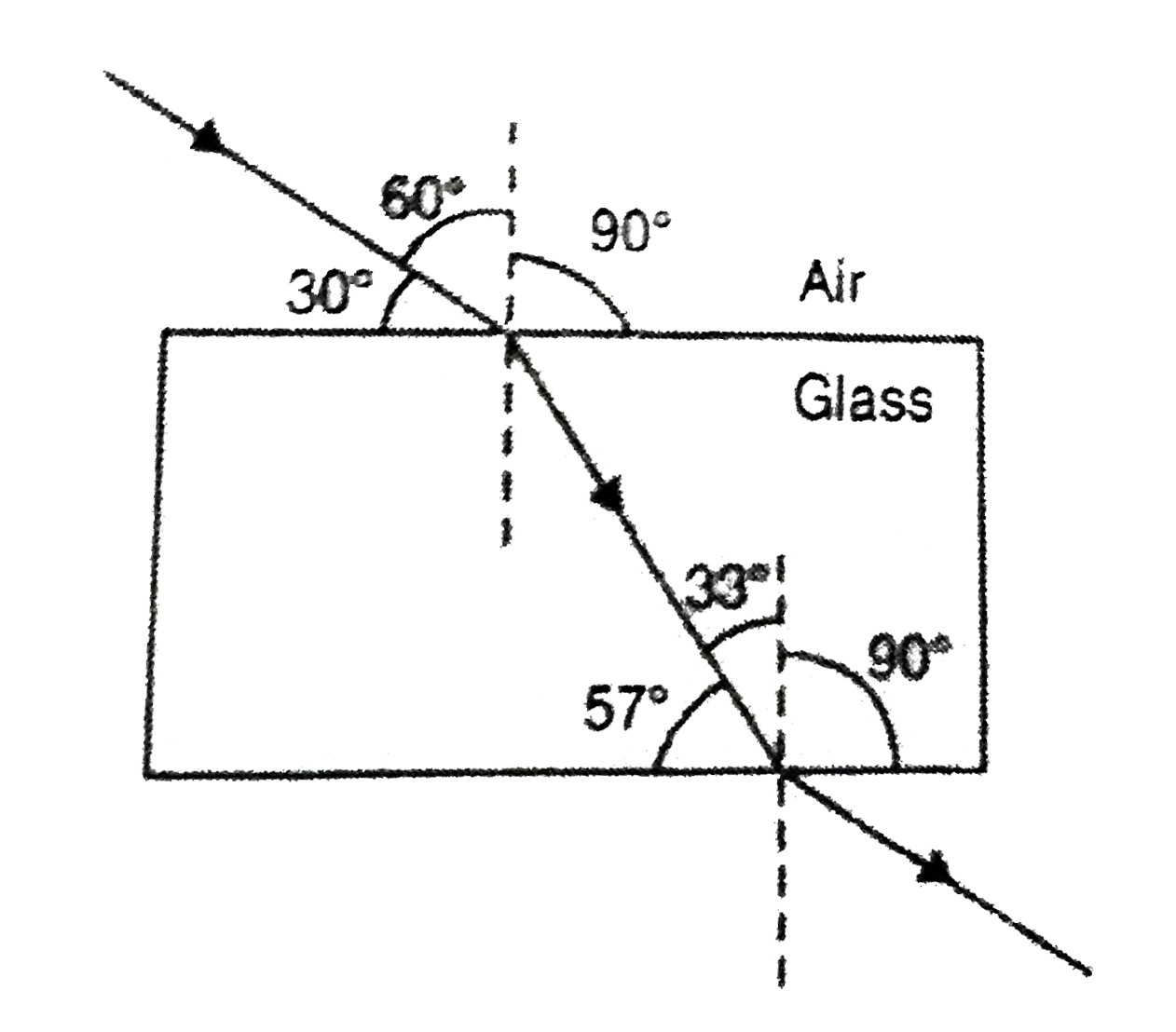 A60∘B33∘C57∘D30∘
A60∘B33∘C57∘D30∘
When rays of light are incident on a glass slab, then the incident ray and emergent ray are ____ to each other.
View SolutionWhite light is incident normally on a glass slab. Inside the glass slab,
View SolutionWhen rays of light are incident on a glass slab, then the incident ray and emergent ray are ……….. To each other.
View SolutionA ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40∘ with the surface. The angle of refraction in glass is
View SolutionA ray of light is incident on a glass slab making an angle of 30∘ with the surface. The angle of refraction in glass, if the refractive index of flass is 1.6 , is
View Solution
