A particle is projected in such a way that it follows a curved path with constant acceleration a. For finite interval of motion. Which of the following options may be correct : Vector u = initial velocity vector a = acceleration of particle vector v = instant velocity for t > 0
Correct option A DExplanation:If vector|a x u| ≠ 0 particle will not follow curved path. Above described motion is a projectile motion
Related Solutions
A particle is projected in such a way that it follows a curved path with constant acceleration vec(a) . For finite interval of motion. Which of the following option (s) may be correct : vec(u)= initial velocity vec(a)= acceleration of particle vec(v)= velocity at tgt0
View SolutionA particle is projected in such a way that it follows a curved path with constant acceleration . For finite interval of motion. Which of the following option may be correct
initial velocity acceleration of particle velocity at
View SolutionInitial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle
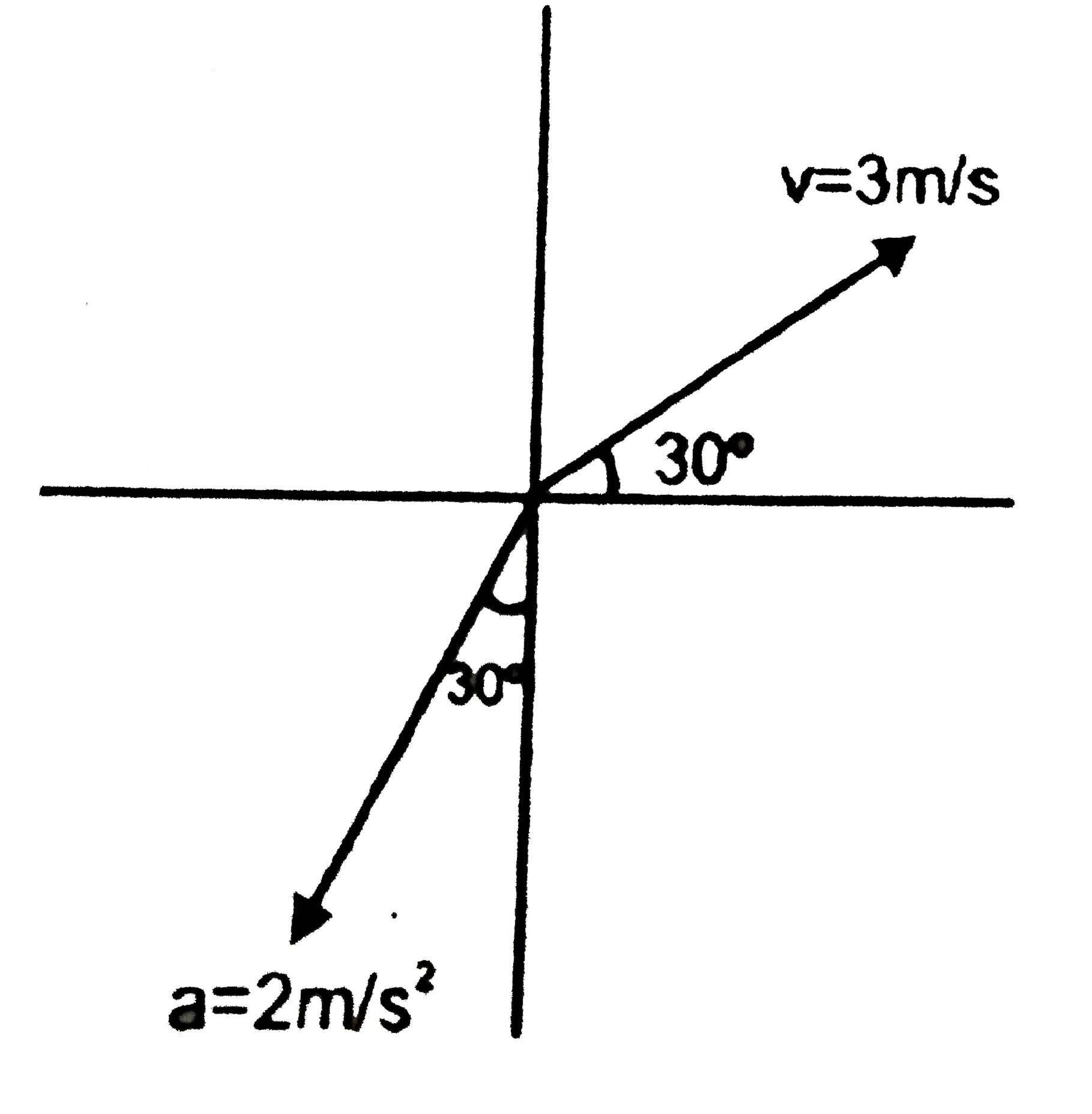
View SolutionInitial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle
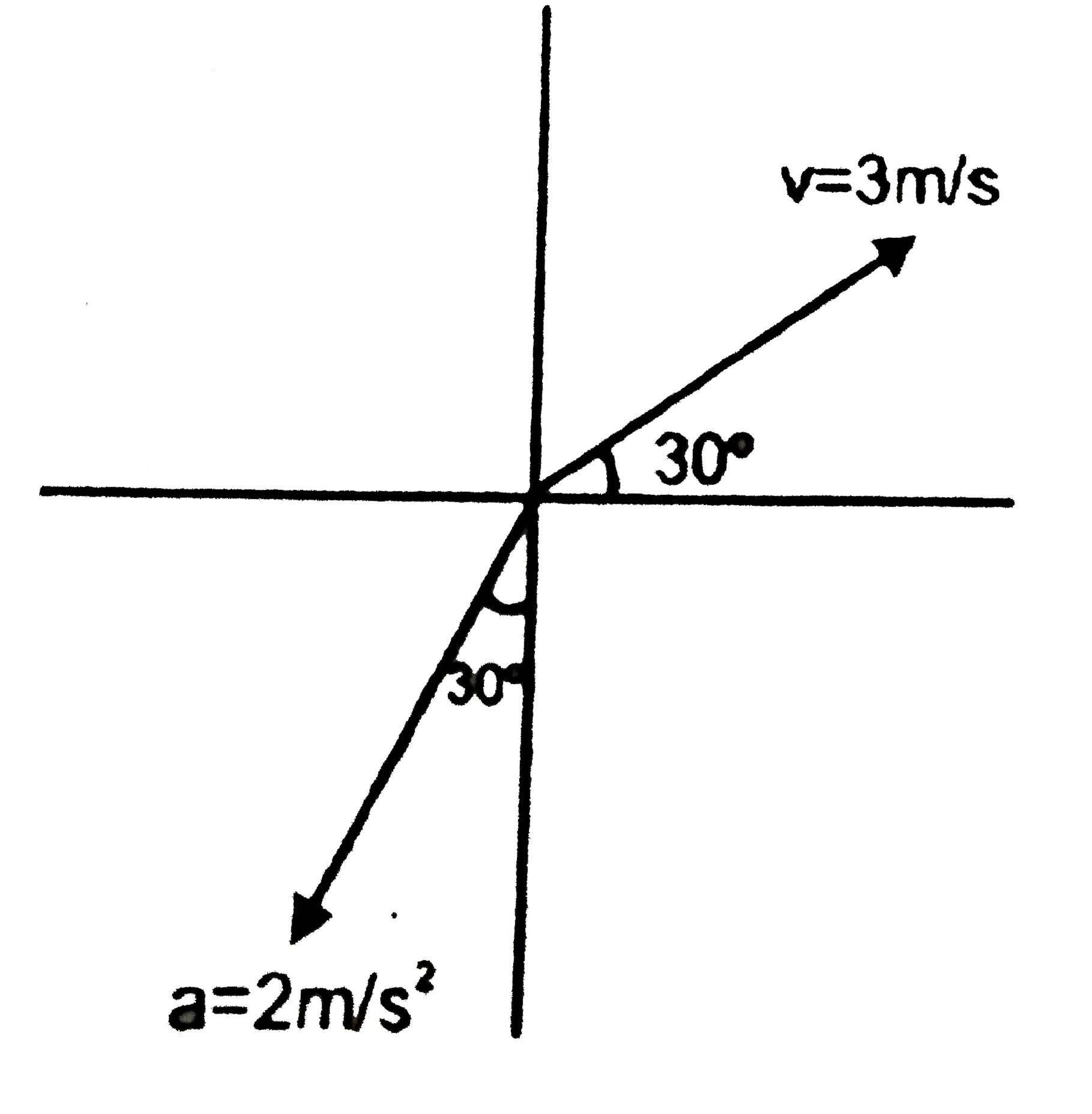
View SolutionThe acceleration vector of a particle moving with a uniform velocity is a ____ vector.
View SolutionA particle is projected with velocity u at angle with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected with velocity u at angle theta with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected with velocity u at angle theta with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionIf the angle (theta) between velocity vector and the acceleration vector of a moving particle is 90^(@) lt theta lt 180^(@) , then the path of the particle is
View SolutionThe velocity of a particle at an instant "t" is v=u+at ,where u is initial velocity and a is constant acceleration.The v -t graph are
View SolutionA particle is moving in circular path with constant acceleration. In time t after the beginning of motion the direction of net acceleration is at to the radius vector at that instant. The angular acceleration of the particle at that time t is
View Solutionकिसी एकसमान वृत्तीय गति में वेग सदिश एवं त्वरण सदिश इस रूप में संबंधित होते है -
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from to second of its motion.
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View SolutionA particle starts moving at t = 0 in a circle of radius R = 2m with constant angular acceleration of a - 3 "rad/sec"^(2) . Initial angular speed of the particle is 1 rad/sec. At time t_(0) the angle between the acceleration vector and the velocity vector of the particle is 37^(@) . What is the magnitude of the acceleration of the particle at t_(0) ?
View SolutionRepresent position vector of a particle in terms of velocity and acceleration vectors.
View SolutionIn uniform circular motion, velocity vector and acceleration vector are
View SolutionIn uniform circular motion, the velocity vector and acceleration vector are
View Solution