A particle is moving in circular path with constant acceleration. In time t after the beginning of motion the direction of net acceleration is at 30∘ to the radius vector at that instant. The angular acceleration of the particle at that time t is
3t2
1t2
√3t
√3t2
The correct Answer is:D
To solve the problem, we need to find the angular acceleration (α) of a particle moving in a circular path with constant acceleration, given that the net acceleration makes an angle of 30 degrees with the radius vector at time t.
1. Understanding the Components of Acceleration:
- The net acceleration (A) of the particle can be broken down into two components:
- Tangential acceleration (At), which is directed along the tangent to the circular path.
- Centripetal acceleration (Ac), which is directed towards the center of the circular path.
- Given that the angle between the net acceleration and the radius vector is 30 degrees, we can use trigonometric relationships to express these components.
2. Using Trigonometry:
- From the angle given (30 degrees), we can write:
tan(30∘)=AtAc
- We know that tan(30∘)=1√3. Therefore, we can express this relationship as:
AtAc=1√3
3. Expressing Accelerations in Terms of Angular Acceleration:
- The tangential acceleration At can be expressed as:
At=αr
- The centripetal acceleration Ac can be expressed as:
Ac=ω2r
- Substituting these into our earlier equation gives:
αrω2r=1√3
- The radius r cancels out, leading to:
αω2=1√3
4. Relating Angular Velocity to Angular Acceleration:
- We know that the angular velocity ω can be expressed in terms of angular acceleration α and time t:
ω=αt
- Substituting this into the equation αω2=1√3 gives:
α(αt)2=1√3
- This simplifies to:
αα2t2=1√3
- Cancelling one α from the numerator and denominator, we have:
1αt2=1√3
5. Solving for Angular Acceleration:
- Rearranging the equation gives:
αt2=√3
- Therefore, the angular acceleration α is:
α=√3t2
Final Answer:
The angular acceleration of the particle at time t is:
α=√3t2
- The net acceleration (A) of the particle can be broken down into two components:
- Tangential acceleration (At), which is directed along the tangent to the circular path.
- Centripetal acceleration (Ac), which is directed towards the center of the circular path.
- Given that the angle between the net acceleration and the radius vector is 30 degrees, we can use trigonometric relationships to express these components.
- From the angle given (30 degrees), we can write:
tan(30∘)=AtAc
- We know that tan(30∘)=1√3. Therefore, we can express this relationship as:
AtAc=1√3
- The tangential acceleration At can be expressed as:
At=αr
- The centripetal acceleration Ac can be expressed as:
Ac=ω2r
- Substituting these into our earlier equation gives:
αrω2r=1√3
- The radius r cancels out, leading to:
αω2=1√3
- We know that the angular velocity ω can be expressed in terms of angular acceleration α and time t:
ω=αt
- Substituting this into the equation αω2=1√3 gives:
α(αt)2=1√3
- This simplifies to:
αα2t2=1√3
- Cancelling one α from the numerator and denominator, we have:
1αt2=1√3
- Rearranging the equation gives:
αt2=√3
- Therefore, the angular acceleration α is:
α=√3t2
The angular acceleration of the particle at time t is:
α=√3t2
Topper's Solved these Questions
Similar Questions
A particle is moving in a circular orbit when a constant tangential acceleration. After 2s from the beginning of motion, angle between the total acceleration vector and the radius E becomes 45∘. What is the angular acceleration of the particle?
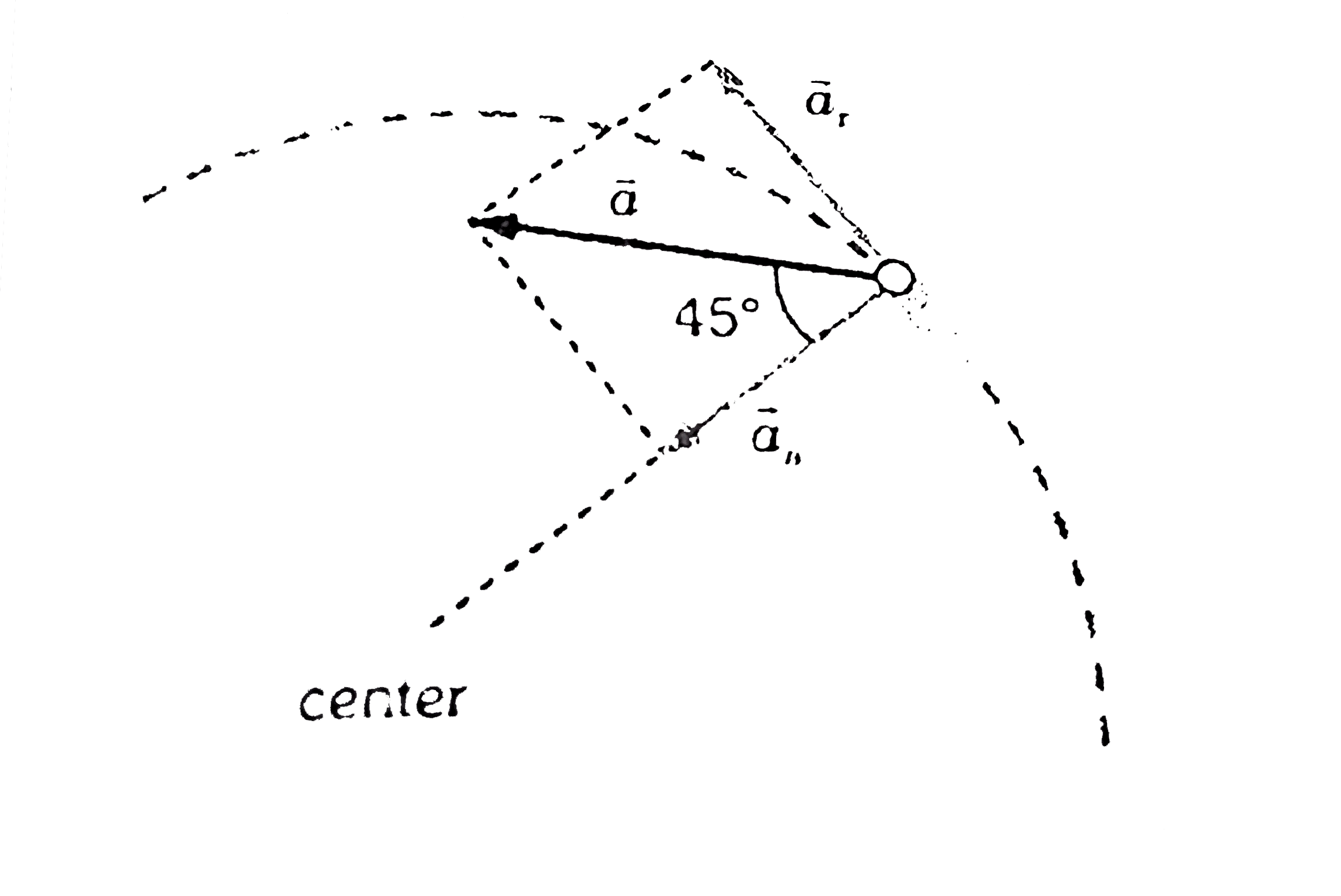
View SolutionIf a particle is moving on a circular path with constant speed, then the angle between the direction of acceleration and its position vector w.r.t. centre of circle will be
View Solution
Knowledge Check
A particle is moving on a circular path with constant speed, then its acceleration will be
AZeroBExternal radial accelerationCInternal radial accelerationDConstant accelerationFor the previous question, the acceleration of the particle at any time t is :
A−0.8m/s2B0.8m/s2C−0.6m/s2D0.5m/s2For the previous question, the acceleration of the particle at any time t is :
A−0.8m/s2B0.8m/s2C−0.6m/s2D0.5m/s2
A particle is moving in a circular orbit with a constant tangential acceleration. After a certain time t has elapsed after the beginning of motion, the between the total acceleration a and the direction along the radius r becomes equal to 45∘. What is the angular acceleration of the particle.
View SolutionA particle revolves round a circular path with a constant speed the acceleration of the particle is :
View SolutionA particle revolves round a circular path. The acceleration of the particle is
View SolutionA particle is revoiving in a circular path of radius 25 m with constant angular speed 12 rev/min. then the angular acceleration of particle is
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View Solution
