A musical instrument is made using four different metal strings. 1 2 3 and 4 with mass per unit length μ 2μ 3μ and 4μ respectively. The instrument is played by vibrating the strings by varying the free length in between the range L0 and 2L0. It is found that in string-1 μ at free length L0 and tension T0 the fundamental mode frequency is f0.List-I gives the above four strings while List-II lists the magnitude of some quantity.List-IList-III String-1 μ P 1II String-2 2μQ 1/2III String-3 3μS 1/ 3IV String-4 4μT 3/16U 1/16If the tension in each string is T0 the correct match for the highest fundamental frequency in f0 units will be A I → P II → R III → S IV → QB I → Q II → P III → R IV → TC I → Q II → S III → R IV → PD I → P II → Q III → T IV → S
Correct option A I → P II → R III → S IV → QExplanation:For all highest fundamental is when length is L0
Related Solutions
A musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length
respectively. The instrument is played by vibrating the strings by varying the free length in between the range
. It is found that in string-1
at free length and tension the fundamental mode frequency is .
List-I gives the above four strings while list-II lists the magnitude of some quantity.
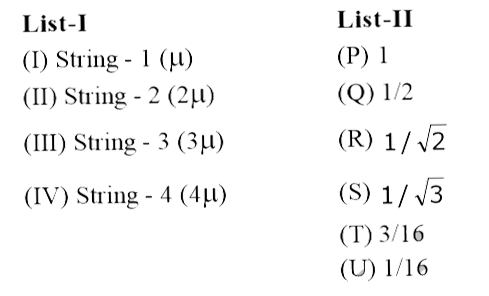
If the tension in each string is , the correct match for the highest fundamental frequency in units will be -
View SolutionA musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length mu,2mu,3mu and 4mu respectively. The instrument is played by vibrating the strings by varying the free length in between the range L_0 and 2L_0 . It is found that in string-1 (mu) at free length L_0 and tension T_0 the fundamental mode frequency is f_0 . List-I gives the above four strings while list-II lists the magnitude of some quantity. If the tension in each string is T_0 , the correct match for the highest fundamental frequency in f_0 units will be -
View SolutionA musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length mu,2mu,3mu and 4mu respectively. The instrument is played by vibrating the strings by varying the free length in between the range L_0 and 2L_0 . It is found that in string-1 (mu) at free length L_0 and tension T_0 the fundamental mode frequency is f_0 . List-I gives the above four strings while list-II lists the magnitude of some quantity. The length of the strings 1,2,3 and 4 are kept fixed at L_0 ,(3L_0)/2,(5L_0)/4 and (7L_0)/4 , respectively . S trings 1,2,3 and 4 are vibrated at their 1^(st), 3^(rd), 5^(th) and 14^(th) harmonics, respectively such that all the strings have same frequency. The correct match for the tension in the four strings in the units of T^0 will be -
View Solutionएक वाद्य - यन्त्र को चार भिन्न धातु की तारों 1 , 2 , 3 और 4 से बनाया गया है , जिनके एकांक लम्बाई के द्रव्यमान ( Mass per unit length ) क्रमशः ,2,3 तथा 4 हैं । इस यन्त्र के तारों को मुक्त लम्बाई . से के बीच परिवर्तित करते हुए कंपित करके बजाया जाता है । पाया जाता है कि तार -1 ( u) की मुक्त लम्बाई , पर तनाव के कारण मूल विधा की आवृत्ति है ।
सूची- I में ऊपर दी गयी चार तारें हैं । सूची- II में किसी मात्रा का परिमाण है ।

तार 1 , 2 , 3 और 4 की लम्बाइयों का मान क्रमशः और है । तार 1 , 2 , 3 और 4 को क्रमशः उनकी प्रथम ( 1st ) , तृतीय ( 3rd ) , पंचम ( 5th ) तथा चौदहवीं ( 14th ) गुणावृत्तियों पर इस तरह से कंपित करते हैं कि सभी तारों की आवृत्तियाँ समान रहती हैं । चारों तारों के तनाव का इकाई में सही मिलान हो
View SolutionThe frequency of vibration of a string depends on, (i) tension in the string (ii) mass per unit length of string, (iii) vibrating length of the string. Establish dimension the relation for frequency.
View SolutionThe frequency of vibration of a string depends of on, (i) tension in the string (ii) mass per unit length of string, (iii) vibrating length of the string. Establish dimensionally the relation for frequency.
View SolutionA string of mass per unit length "0.2 kg m"^(-1) and length 0.6 m is fixed at both ends such that it has a tension of 80 N. If the string is vibrating in its second overtone mode, then the frequency of the string is
View SolutionThe frequency of vibration (v) of a string may depend upon length (I) of the string, tension (T) in the string and mass per unit length (m) of the string. Using the method of dimensions, derive the formula for v.
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as as shown in the figure. The frequency of standing waves produced in the string is in the ratio , when both the strings are vibrating in their fundamental mode. If the mass per unit length of string is , calculate the mass per unit length of the other string.
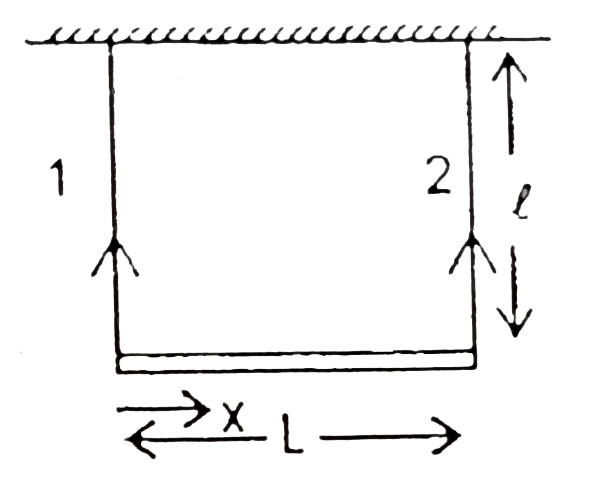
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as as shown in the figure. The frequency of standing waves produced in the string is in the ratio , when both the strings are vibrating in their fundamental mode. If the mass per unit length of string is , calculate the mass per unit length of the other string.

View SolutionLength of string og musical instrument is varied from to in 4 different cases. Wire is made of different materials of mass per unit length respectively. For first case (string -1) length is , Tension is then fundamental frequency is for second case length of the string is (Harmonic), for thid case length of the string is ( Harmonic) and for the fouth case length of the string is ( harmonic). if frequency of all is same then tension in string in terms of will be:
View SolutionA string on a musical instrument is 50 cm long and its fundamental frequency is 270 Hz. If the desired frequency of 1000 Hz, is to be produced, the required length of the string is
View SolutionA string in a musical instrument is 50 cm long and its fundamental frequency is 800 Hz. If a frequency of 1000 Hz is to be produced, then required length of string is
View SolutionA string in a musical instrument is 50 cm long and its fundamental frequency is 800 Hz. If a frequency of 1000 Hz is to be produced, then required length of string is :
View SolutionA string on a musical instrument is 50 cm long and its fundamental frequency is 270 Hz. If the desired frequency of 1000 Hz, is to be produced, the required length of the string is
View SolutionA string in a musical instrument is 50 cm long and its fundamental frequency is 270 Hz. If the desired frequency of 1000 Hz is to be produced, the required string length is
View SolutionA string in a musical instrument is 50 cm long and its fundamental frequency is 800 Hz. If a frequency of 1000 Hz is to be produced, then required length of string is
View SolutionA string in musical instrument is 50 cm long and its fundamental frequency is 800 Hz. If a frequency of 1000 Hz is to be produced, then required length of string is:
View Solutionएक वाद्य - यन्त्र को चार भिन्न धातु की तारों 1 , 2 , 3 और 4 से बनाया गया है , जिनके एकांक लम्बाई के द्रव्यमान ( Mass per unit length ) क्रमशः , , तथा हैं । इस यन्त्र के तारों को मुक्त लम्बाई से के बीच परिवर्तित करते हुए कंपित करके बजाया जाता है । पाया जाता है कि तार की मुक्त लम्बाई , पर तनाव के कारण मूल विधा की आवृत्ति है ।
सूची- I में ऊपर दी गयी चार तारें हैं । सूची- II में किसी मात्रा का परिमाण है ।

तार 1 , 2 , 3 और 4 की लम्बाइयों का मान क्रमशः और है । तार 1 , 2 , 3 और 4 को क्रमशः उनकी प्रथम ( 1st ) , तृतीय ( 3rd ) , पंचम ( 5th ) तथा चौदहवीं ( 14th ) गुणावृत्तियों पर इस तरह से कंपित करते हैं कि सभी तारों की आवृत्तियाँ समान रहती हैं । चारों तारों के तनाव का इकाई में सही मिलान हो
View SolutionThe frequency of fundamental mode of vibration of a stretched string fixed at both the ends is 25 Hz. If the string is made to vibrate with 7 nodes , what is the frequency of vibration ? If the length of string is 3 m , what is the frequency of the 4th harmonic ?
View Solution