A musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length
μ,2μ,3μand4μ respectively. The instrument is played by vibrating the strings by varying the free length in between the range
L0and2L0. It is found that in string-1
(μ) at free length L0 and tension T0 the fundamental mode frequency is f0 .
List-I gives the above four strings while list-II lists the magnitude of some quantity.
If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be -
I→P,II→Q,III→T,IV→U
I→P,II→R,III→S,IV→Q
I→P,II→Q,III→R,IV→T
I→T,II→Q,III→R,IV→U
The correct Answer is:A
f1=f0=c12L0=12L0√T0μ
f2=3fo2=3C22L2=3C22×3L02=c2L0=f0
⇒C2L0=C12L0=⇒C2=C12⇒T22μ=14×T0μ
f3=5fo3=5C32×5L04=2C3L0⇒fo=2C3L0
⇒C3=C14⇒T33μ=116×T0μ⇒T3−316T0
f4=14fo4=14C42L4=14×C42×7L04=4C4L0⇒f0=C12L0
⇒C4=C18⇒T44μ=164×T0μ⇒T4=T416
Correct option is (A)
Topper's Solved these Questions
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (NUMERICAL VALUE TYPE)
21 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (FILL IN THE BLANKS)
17 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (PARAGRAPH TYPE)
6 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
Similar Questions
String-1 is connected with string-2. The mass per unit length in string-1 is μ1 and the mass per unit length in string-2 is 4μ1. The tension in the strings is T. A travelling wave is coming from the left. What fraction of the energy in the incident wave goes into string-2 ?

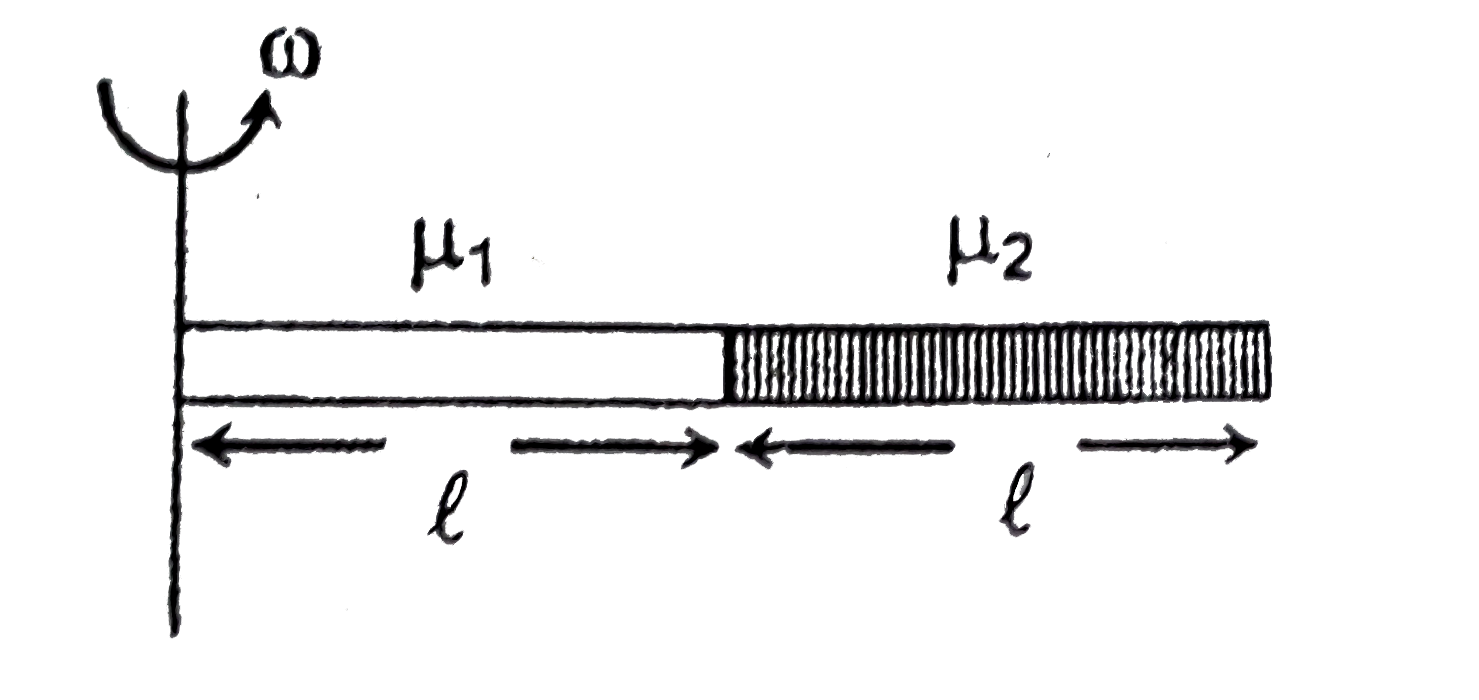
View SolutionTwo thin rods of same length l but of different uniform mass per unit length μ1 and μ2 respectively are joined together. The system is ortated on smooth horizontal plane as shown in figure. The tension at the joint will be
View SolutionThe frequency of vibration of string depends on the length L between the nodes, the tension F in the string and its mass per unit length m. Guess the expression for its frequency from dimensional analysis.
View SolutionWhen a string is divided into three segments of length l1,l2 and l3 the fundamental frequencies of these three segments are f1,f2 and f3 respectively. The original fundamental frequency f of the string is
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.

Determine the tension in the string.
View SolutionA dielectric slab is attached to a string of mass per unit length μ, whose other end is fixed to a wall. It has square plates of side b and separation between the plates is d. Find the fundamental frequency of vibration

View SolutionThe frequency v of the stretched string may depend on (i) the length of the vibrating segment 1 (ii) the tension in the string and (iii) the mass per unit length m. Show that v∝1l√Fm.
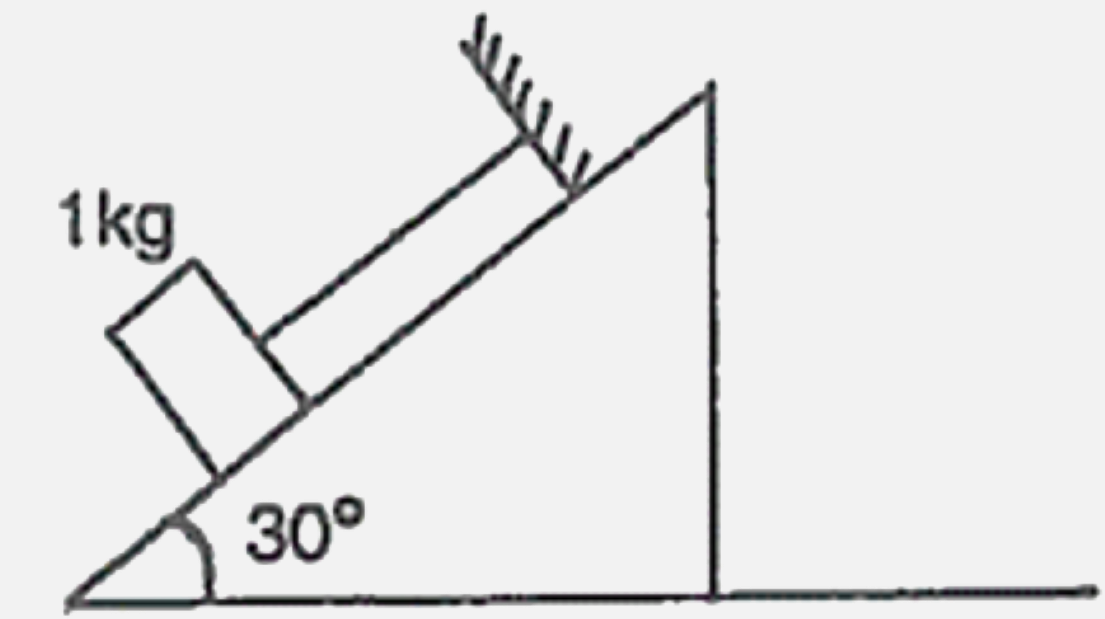
View SolutionThe coefficient of friction between two surface is μ=0.8. The tension in the string as shown in the figure is
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
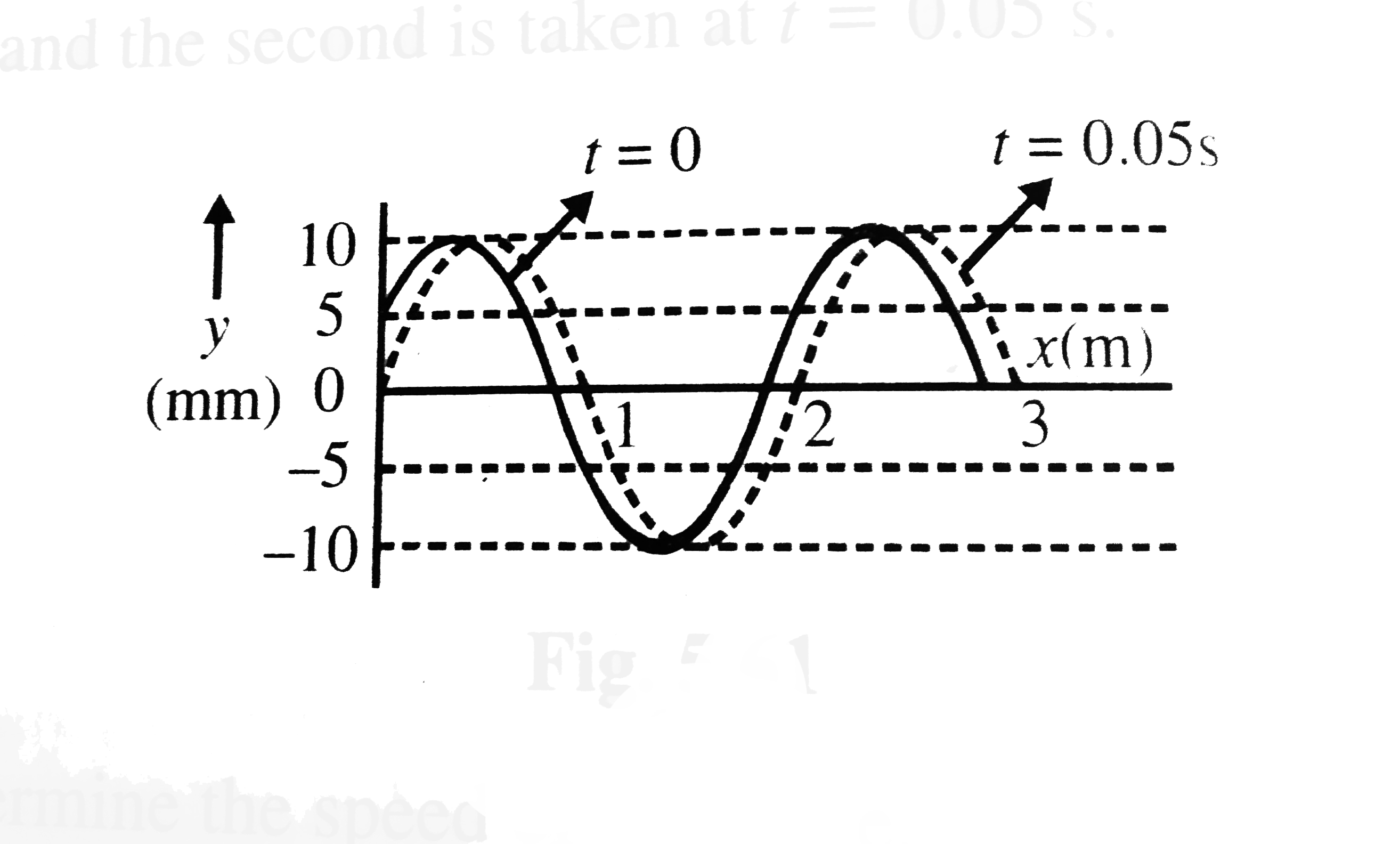
Determine the frequency of the wave.
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
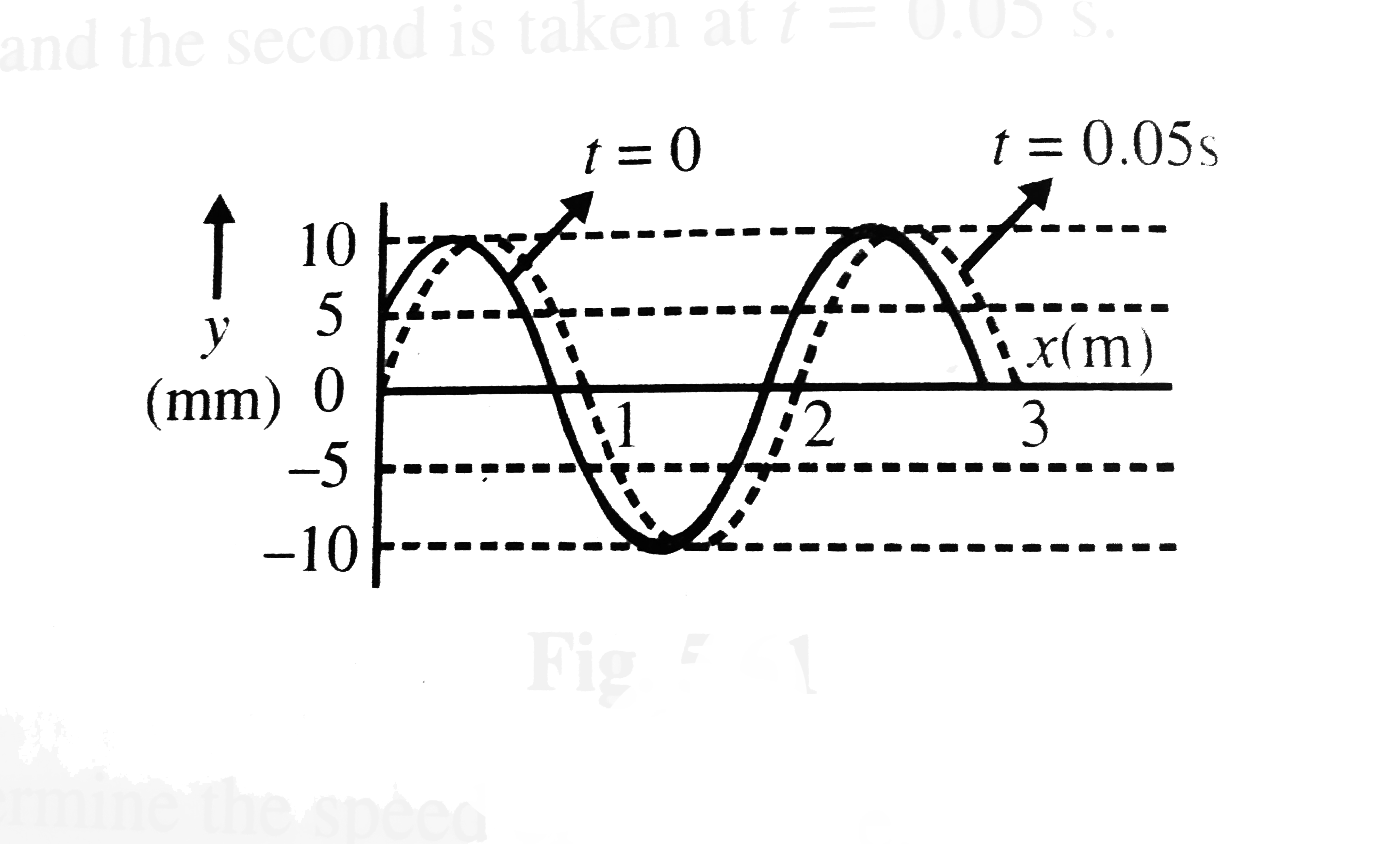
Determine the equation of the wave.
View Solution
