A particle of mass m and speed v hits a rod of length l and mass m at a point l/3 from its fixed support as shown and sticks to it. Angular velocity of rod just after collision isA v/lB 3v/4lC v/2lD 2V/l
Correct option B 3v/4lExplanation:
Related Solutions
A uniform rod of length lies on a smooth horizontal table. The rod has a mass . A particle of mass moving with speed strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass and the angular, velocity of the system about the centre of mass after the collision.
View SolutionA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of and sticks to it. The angular velocity of system after collision is-
View SolutionA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45^@ and sticks to it. The angular velocity of system after collision is-
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v_0 , hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity , hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the angular momentum of the particle and of then about the centre of mass C before the collision.
View SolutionA particle of mass m is moving perpendicular to a rod of length L kept on a frictionless horizontal surface and collides at a distance L/4 from the centre of rod. Particle comes to state of rest just after collision. Mass of rod is M and speed of particle before collision is u. Let v is the velocity of centre of rod after collision and is angular velocity attained by the rod. Find (Lomega)/(v)
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the centre of mass C of the system constituting 'the rod plus the particle'.
View SolutionA rod of mass m,length l pivoted at its centre is free to rotate in a vertical plane.The rod is at rest and is in vertical position.A bullet of mass m/2 moving horizontally with speed v strikes and sticks to one end of the rod. Angular velocity of system just after collision is
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of length lies on a smooth horizontal table. The rod has a mass . A particle of mass moving with speed strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to before the collision
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the particle with respect to C before the collision
View SolutionA rod of length and mass is lying on a horizontal frictionless surface. A particle of same mass travelling along the surface hits the rod at distance from with a velocity in a direction perpendicular to rod and sticks to it.
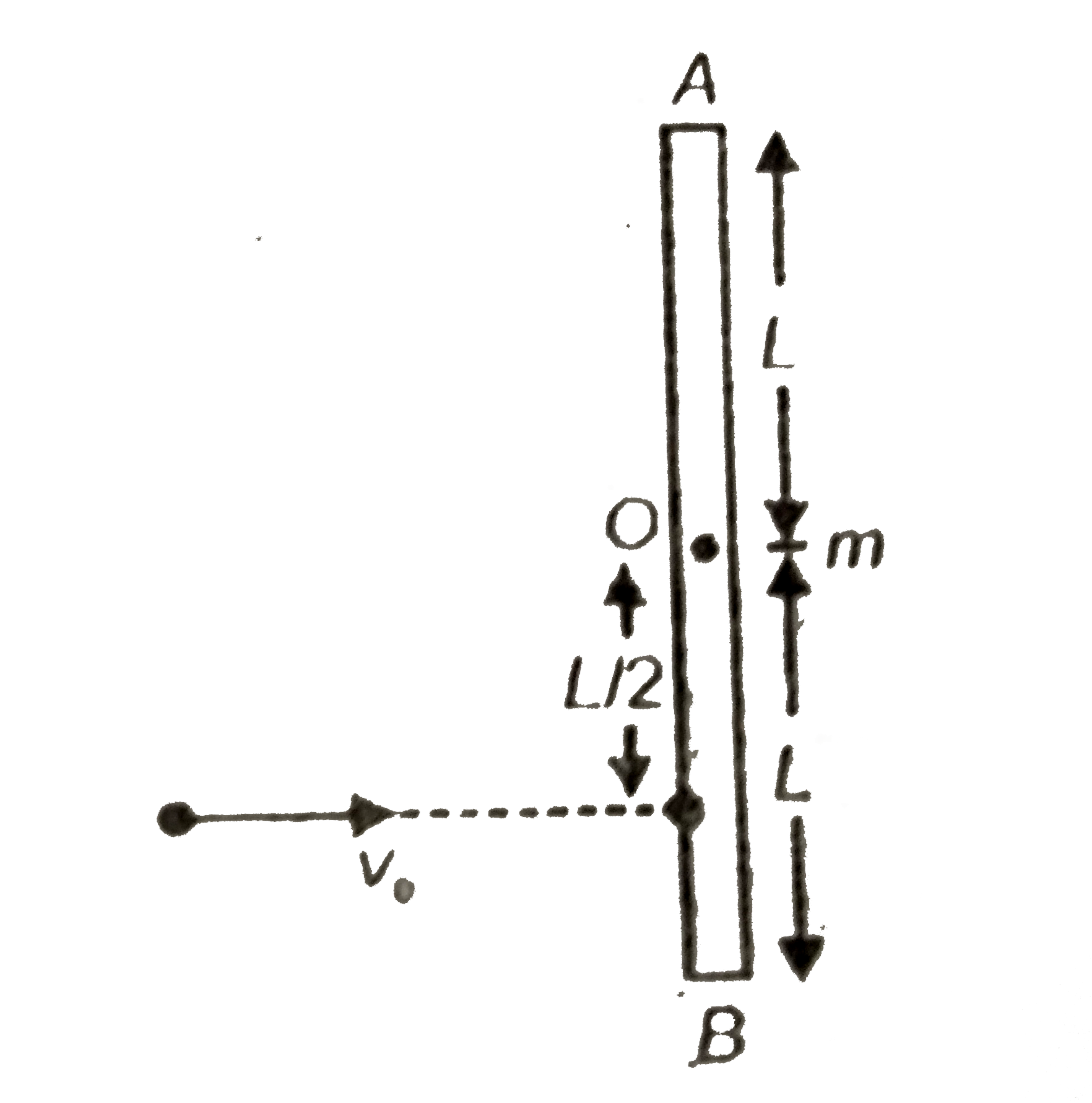
Angular velocity of rod just after collision is
View SolutionA rod of length and mass is lying on a horizontal frictionless surface. A particle of same mass travelling along the surface hits the rod at distance from with a velocity in a direction perpendicular to rod and sticks to it.

Angular velocity of rod just after collision is
View SolutionA rod of length and mass is lying on a horizontal frictionless surface. A particle of same mass travelling along the surface hits the rod at distance from with a velocity in a direction perpendicular to rod and sticks to it.

Angular velocity of rod just after collision is
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the rod with respect to C before the collision
View SolutionA uniform rod of length lambda lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out. The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View Solution