A 0.1 -kilogram block is attached to an initially unstretched spring of force constant k = 40 newtons per meter as shown. The block is released from rest at time t = 0.What is the amplitude in meters of the resulting simple harmonic motion of the block?A 1/40mB 1/20mC 1/4mD 1/2mE 1m
Correct option A 1/40m At the current location all of the energy is gravitational potential. As the spring stretches to its max location all of that gravitational potential will become spring potential when it reaches its lowest position. When the box oscillates back up it will return to its original location converting all of its energy back to gravitational potential and will oscillate back and forth between these two positions. As such the maximum stretch bottom location represents twice the amplitude so simply halving that max ∆x will give the amplitude. Finding the max stretch: The initial height of the box h and the stretch ∆x have the same value h=∆x U = Usp mg∆x1 = ½k∆x12 mg = ½ k∆x1 ∆x1 = .05m. This is 2A so the amplitude is 0.025 m or 1/40 m. Alternatively we could simply find the equilibrium position measured from the initial top position based on the forces at equilibrium and this equilibrium stretch measured from the top will be the amplitude directly. To do this: Fnet = 0 Fsp = mg k∆x2 = mg ∆x2 = 0.025m which is the amplitude
Related Solutions
Two blocks of mass m and 2m are kept on a smooth horizontal surface. Theya are connected by an ideal spring of force constant k. Initially the spring is unstretched. A constant force is applied to the heavier block in the direction shown in figure. Suppose at time t displacement of smaller block is then displacement of the heavier block at this moment would be
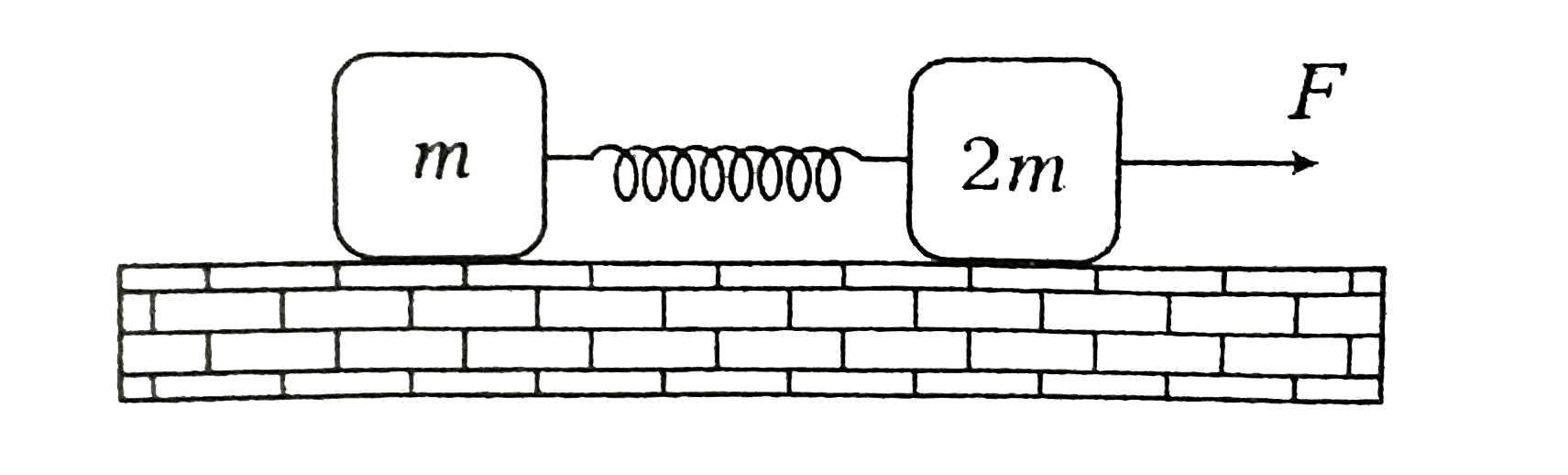
View SolutionTwo blocks of mass m and 2m are kept on a smooth horizontal surface. Theya are connected by an ideal spring of force constant k. Initially the spring is unstretched. A constant force is applied to the heavier block in the direction shown in figure. Suppose at time t displacement of smaller block is then displacement of the heavier block at this moment would be

View SolutionTwo blocks of mass m and 2m are kept on a smooth horizontal surface. Theya are connected by an ideal spring of force constant k. Initially the spring is unstretched. A constant force is applied to the heavier block in the direction shown in figure. Suppose at time t displacement of smaller block is x_(1) then displacement of the heavier block at this moment would be
View SolutionIn the figure shown, the system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m.
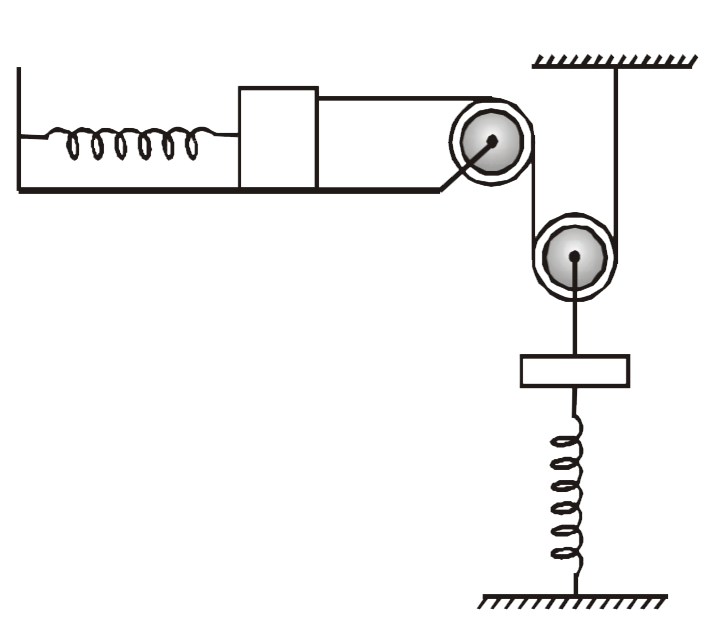
Maximum speed of the block placed horizontally is:
View SolutionA block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Fnd the maximum force exerted by the spring on the block.
View SolutionA block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Find the maximum force exerted by the spring on the block.
View SolutionA block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Find the maximum force exerted by the spring on the block.
View SolutionA block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression an block is released from rest. Collision with the wall are elastic.
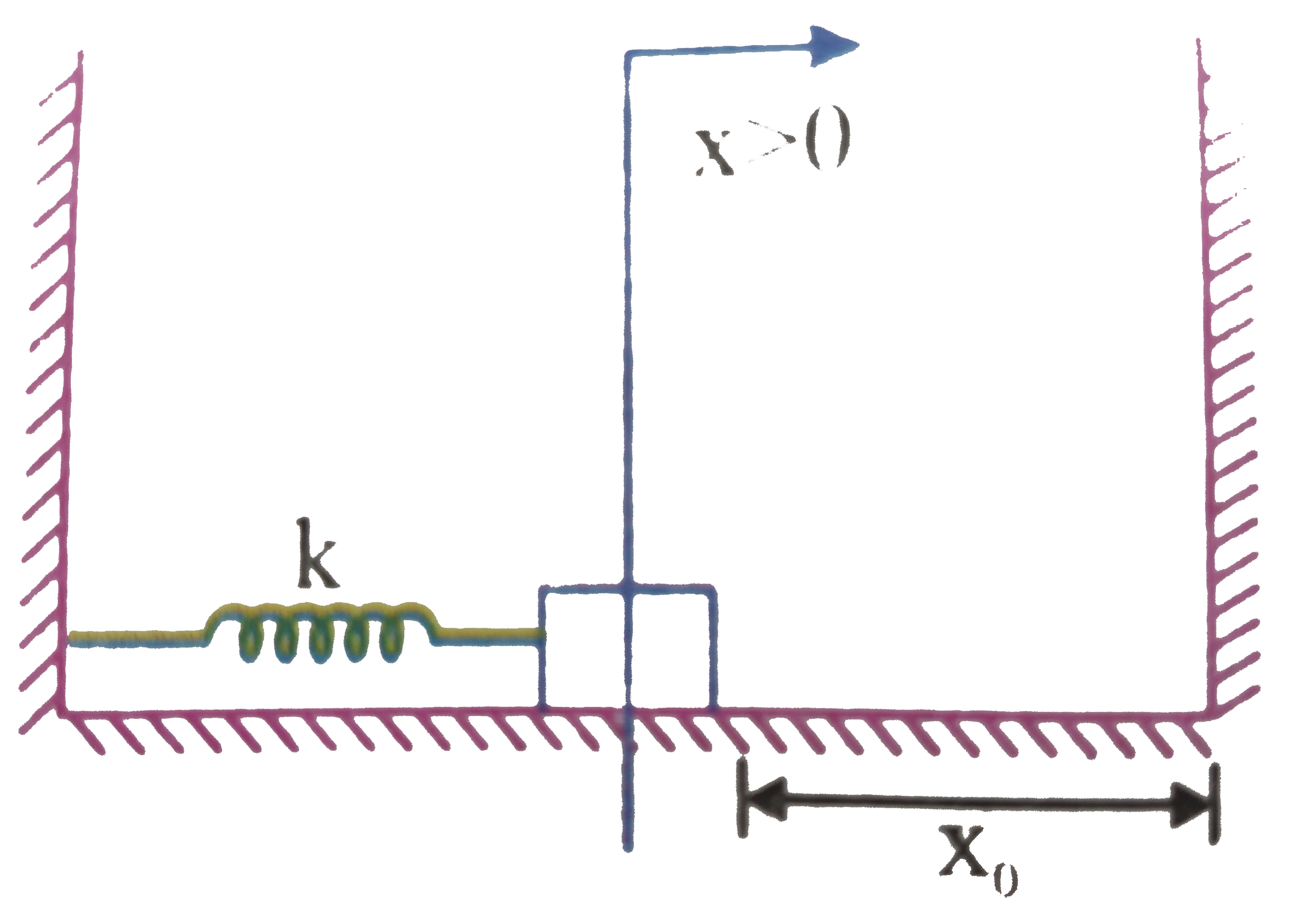
Find the time period of motion of the block:
View SolutionA 20-kg block attached to a spring of spring constant 5Nm^-1 is released from rest at A. The spring at this instant is having an elongation of 1m . The block is allowed to move in smooth horizontal slot with the help of a constant force 50N in the rope as shown. The velocity of the block as it reaches B is (assume the rope to be light)
View SolutionA 20-kg block attached to a spring of spring constant 5Nm^-1 is released from rest at A. The spring at this instant is having an elongation of 1m . The block is allowed to move in smooth horizontal slot with the help of a constant force 50N in the rope as shown. The velocity of the block as it reaches B is (assume the rope to be light)
View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N//m . In the equilibrium position, speed of the block placed horizontally is
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N//m . In the equilibrium position, speed of the block placed horizontally is
View SolutionA block is executing simple harmonic motion of amplitude on a smooth horizontal surface under the restoring force of a spring of spring constant . A block of mass is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together. Find the frequency and the amplitude of the motion.
View SolutionA block of mass m is suspended from a spring of spring constant. Find the amplitude of simple harmonic motion.
View SolutionA block of m mass is moving at a velocity v which is completely unpredictable when connected to the spring of the K force constant by another all-time constant block. What will be the amplitude of the resulting simple periodic motion?
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k'. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm'.
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View Solution