Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a × b.
following figure.
Related Solutions
Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of ax b.
View SolutionShow that the area of the triangle contained between the vectors a and b is one half of the magnitude of .
View SolutionShow that the area of the triangle contained between the vectors a and b is one half of the magnitude of a × b .
View SolutionShow that the area of the triangle contained between the vectors a and b is one half of the magnitude of a xx b .
View SolutionShow that the area of the triangle contained between the vectors is one-half the magnitude of
View SolutionShow that the area of the triangle contained between the vectors a and b is one half of the magnitude of axxb
View SolutionShow that the area of the triangle contained between the vector overset rarr(a ) and overset rarr(b) is one half of the magnitude of overset rarr(a) xx overset rarr(b)
View SolutionShow that area of the triangle contained between vectors veca and vecb is one half of the magnitude of vecaxxvecb .
View SolutionShow that the area of the triangle contained between the vectors veca and vecb is one half of the magnitude of vecaxxvecb .
View SolutionShow that the area of the triangle contained between the vectors veca and vecb is one half of the magnitude of veca xx vecb .
View SolutionShow that the area of the triangle contained between the vector overset rarr(r ) and overset rarr(b) is one half of the magnitude of overset rarr(a) xx overset rarr(b)
View SolutionShow that the area of the triangle contained between the is is one half of the magnitude of .
View SolutionShow that the area of the triangle contained between the vectors J and $ is one haif0fthe magnitude of .
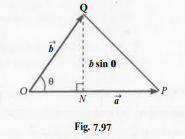
View Solutionદર્શાવો કે સદીશો a અને b થી બનેલ ત્રિકોણનું ક્ષેત્રફળ એ ના મૂલ્યથી અડધું હોય છે.
View Solutionदर्शाइए कि के बीच बने त्रिभुज का क्षेत्रफल के परिमाण का आधा है।
View SolutionThe resultant of two vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between A and B is -
View SolutionThe resultant of two vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between A and B is -
View SolutionThe resultant of two vectors A and B is perpendicular to vector A and its magnitude is equal to half of the magnitude of vector B. Then the angle between A and B is
View SolutionThe resultant of two vectors A and B is perpendicular to vector A and its magnitude is equal to half of the magnitude of vector B . Then the angle between A and B is :
(a) (b)
(c) (d)
View SolutionIf two vectors are represented by the two sides of a triangle , then show that half the magnitude of their cross product will give the area of the triangle .
View Solution